 Z17 Z17  体積(円すい台) 体積(円すい台)
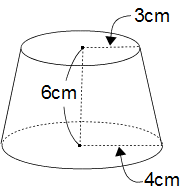
左の図のように、大きな円すいから小さな円すいを切り取った立体があります。上下の円の半径がそれぞれ3cm、4cmで、高さが6cmのとき、この立体の体積は何cm3ですか?(円周率 3.14)
解答 232.36cm3
解説 大きな円すいを復元する図を書いてお読みください。
切り取った小さな円すいと、もともとの大きな円すいは相似で、相似比は底面の半径の比から3:4です。相似な立体の体積比は相似比の3乗で27:64になります。すると切り取ったあとに残されたプリン型の円すい台の体積は64−27=37にあたります。
したがって切り取った小さな円すいの体積の37/27倍が求める円すい台の体積です。小さな円すいの高さは6cmの3倍で18cmです。(小さな円すいと大きな円すいの高さが3:4で、その差分の1が6cmだから)
求める体積は3×3×3.14×18×1/3×37/27=232.36cm3です。
|
 Z16 Z16  面積(相似) 面積(相似)
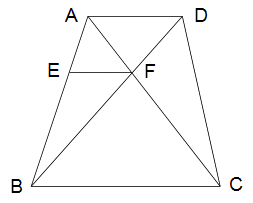 右の図で辺ADと辺BCと辺EFは平行です。また、台形ABCDの面積は三角形ABCの面積の1と2/3倍で、三角形AEFの面積は2と2/5cm2です。 右の図で辺ADと辺BCと辺EFは平行です。また、台形ABCDの面積は三角形ABCの面積の1と2/3倍で、三角形AEFの面積は2と2/5cm2です。
辺ABをAの方に、辺CDをDの方にそれぞれまっすぐ延ばした線が交わる点をGとするとき、三角形GBCの面積は何cm2ですか?
解答 45cm2
解説 題意に沿ってGを用意した図を書いてお読みください。
台形ABCDの面積が三角形ABCの面積の1と2/3倍という条件から、台形ABCD:三角形ABC=5:3です。すると三角形ACD:三角形ABC=2:3とわかり、両者は高さの等しい三角形だから、面積の比と底辺の比が一致し、AD:BC=2:3です。この比は三角形AFDと三角形CFBの相似比になっていて、AF:CF=2:3です。
また、三角形AEFと三角形ABCも相似で、相似比はAF:AC=AF:(AF+FC)=2:(2+3)=2:5、面積比は相似比の2乗だから4:25です。問題の条件から三角形AEF=2と2/5cm2だから、三角形ABC=2と2/5×25/4=15cm2と求められます。
さらに三角形GADと三角形GBCも相似で、AD:BCの2:3が相似比だからGA:GBも2:3です。するとABがGBの1/3であることがわかり、三角形GBCと三角形ABCは高さが等しい三角形だから、三角形ABCの3倍が三角形GBCの面積です。解答は15×3=45cm2です。
|
 Z15 Z15  面積(切り取り) 面積(切り取り)
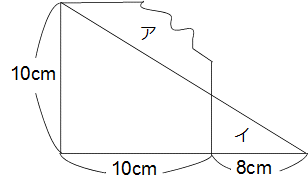
正方形と直角三角形を組み合わせた図形を下の図のように一部を切り取ると、
アとイの部分の面積が等しくなりました。切り取った部分の面積は何cm2ですか?
解答 10cm2
解説 アの下にある台形をウとすれば、アとイが等しいことから、ア+ウ=イ+ウ(直角三角形)です。
イ+ウの直角三角形の面積は18×10÷2=90cm2だから、ア+ウの面積もそれと同じです。
もとの正方形の面積は10×10=100cm2だから、切り取った部分の面積は100−90=10cm2です。
|
 Z14 Z14  面積比(平行移動) 面積比(平行移動)
三角形ABCを辺BCの延長上に平行移動したとき、ア、イ、ウの面積比を簡単な整数で表しなさい。
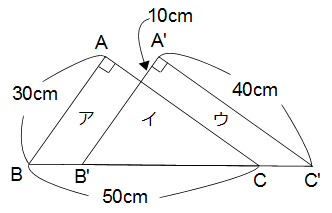
解答 5:4:5
解説 三角形ABCとA'B'C'は合同だから、同じイの部分を除いたという理由でアとウは同じ面積です。
三角形イと三角形ABCは相似で、相似比2:3から面積比は4:9です。三角形アの面積は9−4=5にあたり、
求める面積比は5:4:5です。※もちろん三角形イは三角形A'B'C'とも相似で面積比は4:9です。
|
 Z13 Z13  面積(直角二等辺三角形) 面積(直角二等辺三角形)
下の図のように直角二等辺三角形ABCの中に3つの直角二等辺三角形を作ります。
このとき緑色の線で囲んだ部分の面積は何cm2ですか?
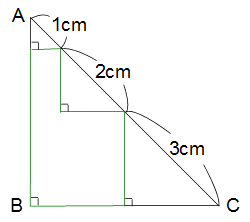
解答 5.5cm2(5と1/2cm2)
解説 普通にいきましょうか。
直角二等辺三角形の面積は、正方形の面積の半分として求めます。
正方形の面積は〈対角線〉×〈対角線〉÷2だから、さらにその半分です。
求める面積
=6×6÷2÷2−(3×3÷2÷2+2×2÷2÷2+1×1÷2÷2)
={6×6−(3×3+2×2+1×1)}÷2÷2
=(36−14)÷2÷2=5.5cm2
|
 Z12 Z12  線分の長さ(相似) 線分の長さ(相似)
下の図のように直角三角形ABCと直角三角形DCBの斜辺(直角と向き合う辺)の交点をEとして、
点EよりBCに垂直な線EFをひきます。このときEFの長さを求めなさい。
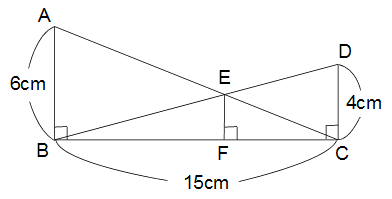
解答 2.4cm(2と2/5cm)
解説
三角形ABEと三角形CDEは相似で、相似比(AB:CD)は6:4→3:2です。
これはBE:DEの比にもなっています。
また三角形BEFと三角形BDCも相似で、相似比はBE:BD=3:(3+2)=3:5です。
これはEF:DCの比でもあるから、EF=4cm×3/5=2.4cmです。
※EFの長さをABの長さとDCの長さの調和平均といいます。
EF=(AB×DC)÷(AB+DC)という公式が知られています。
|
 Z11 Z11  線分の長さ(合同と相似) 線分の長さ(合同と相似)
下の図のような長方形の紙があります。辺AB上に点Eをとり、CEを折り目にして折ると、点Bはちょうど辺AD上にきました。この点をFとするとAFの長さは2cmになりました。BEの長さを求めなさい。
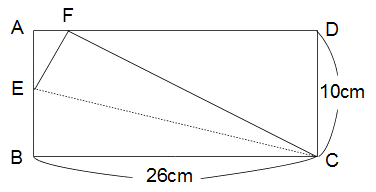
解答 5.2cm(5と1/5cm)
解説 三角形EBCとEFCは合同だから、FC=BC=26cmです。また、角AEF+角AFE、角AFE+角DFCはどちらも90°だから、角AEFと角DFCは等しく、このことから三角形AEFとDFCは相似です。(直角をふくめて2つの角が等しいから)
するとAF:DC=EF:FCが成り立ちます。2:10=EF:26より、EF=5.2cmです。BEはEFと等しいからこれが解答です。慶応義塾の問題でした。
|
 Z10 Z10  円の回転と軌跡 円の回転と軌跡
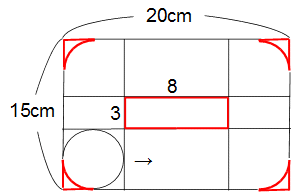
左の図(問題ページ参照)はタテ15cm、横20cmの長方形です。この長方形の内部を半径3cmの円が長方形の辺に沿って1周したとき、円が通り過ぎる部分の面積は何cm2ですか?(円周率 3.14)
解答 268.26cm2
解説
左図のように中央の長方形と四隅の図形の部分が通過できません。
中央の長方形の面積は3×8=24cm2、四隅の図形を1つにまとめた面積は〈1辺6cmの正方形〉−〈半径3cmの円〉=6×6ー3×3×3.14=7.74cm2です。
これらを全体の長方形から引いて、求める面積は15×20−(24+7.74)=300−31.74=268.26cm2です。
|
 Z09 Z09  面積(長方形とおうぎ形) 面積(長方形とおうぎ形)
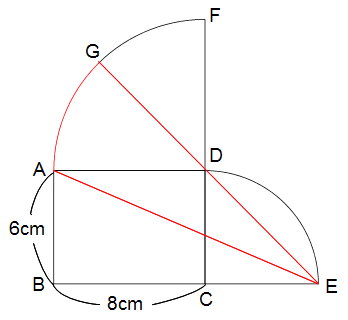
左の図は長方形ABCDに、ADおよびCDを半径とする四分円(円の1/4)を組み合わせたものです。いま、点AとEを結び、2点D、Eを通る直線が弧と交わる点をGとしたとき、赤い線で囲んだ図形AEGの面積は何cm2ですか?(円周率 3.14)
解答 49.12cm2
解説
〈おうぎ形DGA〉+〈三角形CDE〉+〈長方形〉−〈三角形ABE〉を計算します。
8×8×3.14×1/8+6×6×1/2+6×8−14×6×1/2
=8×3.14+18+48−42=8×3.14+24
=25.12+24=49.12cm2 となります。
|
 Z08 Z08  面積の比(正三角形と円) 面積の比(正三角形と円)
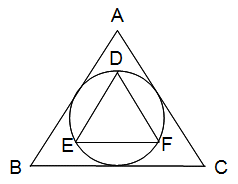
左の図のように大きな正三角形ABCにちょうどぴったり入る円があり、その内側に円にちょうどぴったり入る小さな正三角形DEFがあります。
このとき、2つの正三角形ABCとDEFの面積の比を求めなさい。(円周率 3.14)
解答 4:1
解説 小さい方の正三角形を、E(or F)がAの真下にくるように回転させてみてください。小さい正三角形は大きい正三角形を4等分した大きさになっていることがわかるでしょう。
|
 Z07 Z07  表面積(回転体) 表面積(回転体)
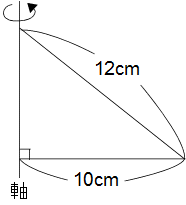
左の図のような三角形を軸のまわりに1回転させてできる立体の表面積は何cm2ですか?(円周率 3.14)
解答 690.8cm2
解説 底面の半径が10cm、母線の長さが12cmの円すいができます。
円すいの表面積は〈底面積〉+〈側面積〉です。
〈底面積〉10×10×3.14
〈側面積〉12×10×3.14 ←母線×底面の半径×3.14
これらを合計して求める表面積は(10×10+12×10)×3.14=220×3.14=690.8cm2です。
|
 Z06 Z06  体積(三角柱の切断) 体積(三角柱の切断)
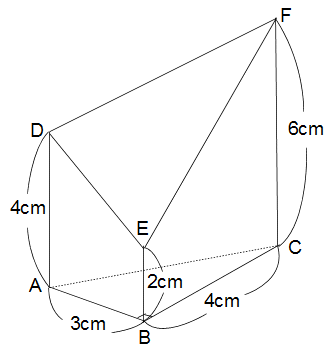 左の図は角ABCが90°、ABが3cm、BCが4cmの三角形ABCを底面とする三角柱を3点D、E、Fを通る平面で斜めに切った立体です。 左の図は角ABCが90°、ABが3cm、BCが4cmの三角形ABCを底面とする三角柱を3点D、E、Fを通る平面で斜めに切った立体です。
この立体の体積は何cm3ですか?
解答 24cm3
解説
このような立体を断頭三角柱といいます。断頭三角柱の体積は、〈底面積〉×〈高さの平均〉で求めます。
この場合は三角形ABCを底面とみて、AD、BE、CFの平均を高さの平均と考えます。
三角形ABCの面積は3×4×1/2=6cm2
AD、BE、CFの平均は(4+2+6)÷3=4cmです。したがって求める体積は6×4=24cm3です。
※断頭三角柱の公式の理由は長くなるのでここでは触れませんが、イメージとしては「図の側面の台形DABEの面積が、底辺をAB(3cm)、高さをDA(4cm)とEB(2cm)の平均(3cm)とみることで求められる」→これを3次元に置きかえたイメージです。
|
 Z05 Z05  角度 角度
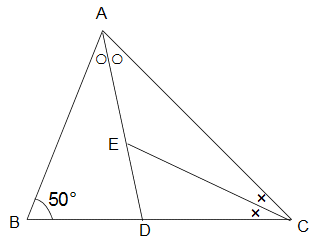
左の図のように三角形ABCで、辺BC上に点Dを、AD上に点Eを角BADと角CADが等しく、角ACEと角DCEが等しくなるようにとります。角ABCが50°のとき、角CEDは何度ですか?
解答 65°
解説
全体の三角形ABCについて角Bが50°だから角Aと角Cの合計、つまり○2コと×2コの合計は180−50=130°です。すると○1コと×1コの合計は130÷2=65°です。角CEDは三角形AECの外角だから○と×の合計と等しくなります。
|
 Z04 Z04  図形の構成 図形の構成
 面積5cm2の正方形のタイルを左の図のようにタテ4個、横4個並べました。 面積5cm2の正方形のタイルを左の図のようにタテ4個、横4個並べました。
図の中にある大小すべての正方形の面積の和は何cm2ですか?
解答 520cm2
解説
一番小さい正方形の1辺を1とすると、
1辺1の正方形が16個→1×1×16=16マス分
1辺2の正方形が9個→2×2×9=36マス分
1辺3の正方形が4個→3×3×4=36マス分
1辺4の正方形が1個→4×4×1=16マス分 以上全部で30個の正方形があり、のべ104マスを使用します。1マスの面積は5cm2だから、求める解答は5×104=520cm2です。
|
 Z03 Z03  面積の比(相似) 面積の比(相似)
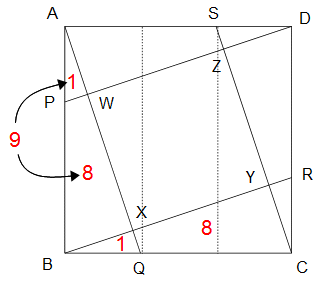
左の図(問題ページ参照)の正方形のABCDで、P、Q、R、Sは各辺を3等分した点です。線分AQ、BR、CS、DPを引いたとき、中央にできる正方形の面積は、正方形ABCDの面積の何倍ですか?
解答 2/5倍(0.4倍)
解説
△APWと△ABXは相似比1:3の相似形です。相似形の面積は相似比の2乗だから△APW:△ABXは1:9です。また、△APWと△BQXは合同で、△ABQの面積は10です。
正方形ABCDを点線のように3等分すると、△ABQは3分の1のさらに半分だから正方形ABCDの6分の1です。したがって正方形ABCDの面積は60です。また、中央にある正方形WXYZの面積は正方形ABCDから△ABXを4つ分引くことで求められます(△ABX、△BCY、△CDZ、△DAWは合同)。これらのことから正方形WXYZの面積は60−9×4=24であり、解答は24÷60=2/5倍です。
|
 Z02 Z02  面積(ひもの先端が動く) 面積(ひもの先端が動く)
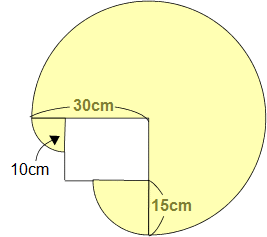 左の図(問題ページ参照)のような長方形の1つの頂点にひもがついています。ひもの長さは30cmです。ひもの先端が動ける部分の面積を求めなさい。ただし、ひもは長方形の内部には入れません。(円周率 3.14) 左の図(問題ページ参照)のような長方形の1つの頂点にひもがついています。ひもの長さは30cmです。ひもの先端が動ける部分の面積を求めなさい。ただし、ひもは長方形の内部には入れません。(円周率 3.14)
解答 2374.625cm2
解説
ひもの動く部分は、左の図のようにおうぎ形が3つになります。
(30×30×3/4+15×15×1/4+10×10×1/4)×3.14
=(2700/4+225/4+100/4)×3.14=3025/4×3.14=756.25×3.14
=2374.625cm2
|
 Z01 Z01  角度 角度
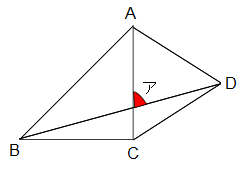
左の図は直角二等辺三角形ABCと正三角形ACDを組み合わせた図形です。角アの大きさは何度ですか?
解答 75°
解説 AC=BC(直角二等辺三角形)AC=CD(正三角形)より、BC=CDで、三角形BCDは二等辺三角形です。角BCD=90+60=150°だから、角CBD=(180−150)÷2=15°です。左下の三角形に注目して、角ア=180−(15+90)=75°です。
|

東京近郊で中学受験を目指すお子様への算数家庭教師はさんじゅつまんにお任せください。
下記リンク「中学受験算数家庭教師について」をお読みになり、そのページ内に設置してあるフォームよりご連絡ください。
|

