 |
第8話「倍数に0は含まない。しかし…」 算数における倍数の定義は「ある整数Aを1倍、2倍、3倍、…のように[自然数]倍した整数」です。たとえば6の倍数は6、12、18、…ですね。このように倍数は1倍から考えますから、気になった人もいるかと思いますが、A×0の0は算数ではAの倍数として考えないことにしています。「5の倍数を小さい順に3つ答えなさい」この問題の正解は5、10、15であり、0、5、10ではありません。 しかしそのこととは別に「5で割ると2余る整数」という場合には、商が0になる場合も含まれるから注意してください。*2÷5=0あまり2 「5で割ると2余る整数」は 5×□+2 (□は任意の整数) の形で表現できますが、□に入れる整数は1からではなく、0から考えます。 「5で割ると2余る一番小さい整数は?」この質問を生徒たちにすると、7と答える生徒が多いですが、残念ながらそれは間違いで、正解は余り自身の2です。5×1+2=7が最小ではなく、5×0+2=2が最小です。出てくる結果が0ではないから、さすがにこれを除外する理由はありません。倍数で0倍の0を考えない影響もあると思いますが、この例は盲点になりがちなようです。ウッカリして解答が1つズレてしまうケースがありますから、受験生の算数をアドバイスなさることがある方は気に留めておいてください。 練習問題 100以下の整数で、6で割ると3余る整数は全部で何個ありますか? *数学では倍数に0を含めたり、さらには負の数(マイナスの数)まで拡張して倍数を考えることがあります。数学では0の両サイドに正負(プラスマイナス)の数が同じように広がっているから、正負の公平さを保つためにそれが必要になる場合もあるでしょうが、算数には負の数がありません。もっとも算数で扱う最小の整数は1ではなく0なので、負の数はともかく、0は倍数と考えても不思議はなさそうですが、おそらく具体的に存在する事がらを大事にする算数だから、無存在を表す整数0は倍数から除外するのでしょう。0を倍数に認めると、どんな2数の最小公倍数も0になってしまうという問題も起こります。2と3の最小公倍数は0? これは違和感ありますよね? 0を倍数としないのは、そうした意味合いを含めた算数のルールという認識でよいでしょう。 *練習問題の解答→最小が6×0+3=3、最大が6×16+3=99です。オレンジ色の数字を求める整数のナンバーと考え、0から16までの整数の個数17個が正解です。(注意・100÷6=16.…の商だけで判断すると1個不足してしまいます) 第7話 ご存知のように算数には方程式という概念はありません。そのため、○○算といった特殊算が多数用意されており、各塾、各先生ごとに文章題における方程式回避にさまざまな工夫を施しています。しかし数多くの文章題に当たっていると、どうしても次のような式に遭遇してしまうことがあるかと思います。 □×12ー32=□×4ー8 方程式の知識があれば□×12ー□×4=−8+32 のように移項を行いたいところですが、算数には移項という概念もありません。このような場合、算数ではイコールの両側で、□の要素と数だけの要素について、それぞれの差を取ると等しくなると指導します。 その際、各要素が+(たし算)のあとかー(引き算)のあとかを見極め、+のあとどうし、ーのあとどうしなら単純に数字(数学でいう絶対値)を引き算して差を考え、+のあと,ーのあとに分かれている場合は、数字(絶対値)をたし算して差を考えることがポイントになります。 上の例の場合は、□の要素は+どうしだから(算数で式の先頭要素がーにはなることはありません)□×12と□×4の差で□×8、数だけの要素は32,8ともにーのあとだから32と8の差で24のように考え、□×8=24→□=24÷8=3と求めます。身近で受験生の算数をアドバイスなさることがある方はぜひ知っておいてくださいね。 練習問題 96ー□×12=□×6+24 *結果的に□がマイナスの数になる等式があれば、この考え方には欠陥があります。ただし、算数では□がマイナスの数になることはないから、その問題が起きたとすれば立式自体に問題があることになります。立式さえ正しければ、算数ではこれで特に問題は起きないでしょう。 *[練習問題の解答]□要素は和を取って18×□、数要素は差を取って72、18×□=72より、□=4です。 第6話 今回は「循環小数を分数に直す方法について」です。 0.AAA…のように小数点以下1ケタが循環する小数は[9分のA]という分数に直せます。0.111…=1/9、0.777…=7/9などです。 0.ABABAB…のように小数点以下2ケタが循環する小数は[99分のAB]という分数に直せます。0.232323…=23/99、0.363636…は36/99を約分して4/11です。 0.ABCABCABC…のように小数点以下3ケタが循環する小数は[999分のABC]という分数に直せます。0.123123123…は123/999を約分して41/333です。 以下、循環部分が伸びても、循環部分と同じケタ数の9を分母に配置し、分子に循環部分をそのまま配置すれば循環小数の分数化ができます。 じつはこのように小数点の直後から循環が起こる循環小数のことを純循環小数といいますが、なかには小数点の後ろに固定部分があり、その先で循環が起こる混循環小数もあります。たとえば0.5333…などです。 混循環小数を分数に直すときは、1=0.5333…とおき、10倍した10=5.333…と100倍した100=53.333…の差を考えるようにします。90=53.333…−5.333…=48(小数点以下は同じだから引くと消えてしまう)。1=48÷90=48/90=8/15です。 循環小数の分数化。とても楽しいのでみなさんも自分で例題を作って考えてみてください。 第5話 1/7(7分の1)という分数を小数に直すと、0.142857142857…というように小数第一位から小数第六位までが繰り返す循環小数(ジュンカン小数)になります。この循環は「石には粉(イシニハコナ)」と覚えるとユニークで忘れないですよ。 では2/7(7分の2)はどうなると思いますか? 2÷7を筆算すると小数第一位には2がたちます。そして以下0.285714…と続き、これは1/7(イシニハコナ)を、ニのところから読み始めた(ニハコナイシ)になっています。スタートの位置が違うだけで同じメンバーの数字が同じ順番を守って回転するのですね。 はい、3/7(7分の3)〜6/7(7分の6)まですべて同じ仕組みになっています。3÷7(3/7)は小数第一位に4がたち、以下0.428571…です。イシニハコナをシから読んでシニハコナイですね。 4÷7(4/7)、5÷7(5/7)、6÷7(6/7)についてはみなさんが電卓で調べてみてください。 *「石には粉」の語呂合わせは桜井進先生のご著書「思わず話したくなる数学」から引用させていただきました。桜井先生Thanks!!! 第4話 1/9(9分の1)という分数を小数に直すと、0.11111…のように小数第一位から無限に1が繰り返す循環小数(ジュンカン小数)になります。電卓で1÷9をやってみてください。 同じように2/9(9分の2)は0.22222…、3/9(9分の3)は0.33333…、4/9(9分の4)は0.44444…となり、以下分子が5、6、7、8になっても同じことです。 さて、では9/9(9分の9)はどうなるのでしょう??? この考え方でいくと0.99999…のように小数第一位から無限に9が繰り返される循環小数になるはずですね。でも待ってくださいよ? 9/9って約分すると整数の1ですねー。 あれ? そうすると0.99999…=1なのでしょうか??? えーと結論から言いますと算数や数学では0.99999…=1であることになっています。これはおそらく納得できる人とできない人で真っ二つに分かれるでしょうね。個人的な意見を書きますと、そもそも0.9から始まっているわけだから、その先にどれだけ9を並べても、最初の出遅れは挽回できず、整数の1よりは微(かす)かに小さい気がしますけどね。みなさんはどのように思ったかな? 結論に賛成? 個人的な私に賛成? 第3話 素数(そすう⇒1とその数自身以外に約数を持たない数)は有名だからみなさんご存知かと思いますが、素数を逆に読んだ数素(すうそ)のことはご存知でしょうか。数素とはその数を逆の方向から読んでも素数になる素数のことです。数素を小さい順にいくつか列挙してみると13, 17, 31, 37, 71, 73, 79, 97, 107, 113,…のようになります。たとえば素数13は逆から31と読んでも素数ですね。なお、素数のことは英語でprime(プライム)といい、この英単語を逆から読むとemirpになるから数素は英語でエマープです。逆から読んでも素数であることを、英単語を逆から読むことで表現したわけですね。そして日本語でもそれをマネしたということでしょう。数学者たちのユニークさが垣間見れるお話です。覚えておいてくださいね(^O^) 第2話 素数についての楽しいお話を紹介します。29と31のように差が2である2つの素数の組を双子素数といいますが、じつはこれ以外にも素数には次のような名前があります。数学者ってユニークですね。 *以下、五つ子素数、六つ子素数もあります。 第1話 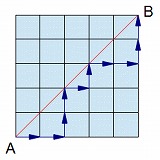 問題 右の図で対角線ABをまたがないように、AからBまで遠回りしないで行く行き方は何通りあるでしょうか? 問題 右の図で対角線ABをまたがないように、AからBまで遠回りしないで行く行き方は何通りあるでしょうか?この問いの答えになる数をカタラン数といいます。正方形の1辺の長さを長くするとカタラン数も大きくなります。第9講座も参考にして、正方形の1辺の長さとそれに対応するカタラン数を考えてみてください。*右図は1辺の長さが5の場合 解答 正方形の1辺の長さ1〜10に対応するカタラン数は次の通りです。 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 上右図の場合、正方形の1辺は5で、AからBまでの対角線をまたがない最短経路は42通りです。 |