 Z30 Z30  角度 角度
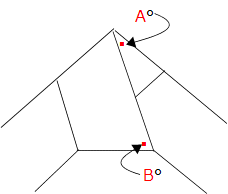
左の図のように、紙テープをゆるみなくしっかり結んだとき、AとBの角度はそれぞれ何度になりますか?
解答と解説 まだ発表していません。がんばってください!
|
 Z29 Z29  角度 角度
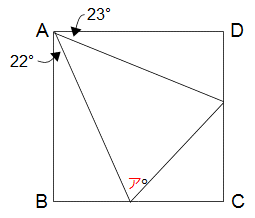
左の図において、アの角は何度になりますか? ただし、四角形ABCDは正方形です。
解答と解説 まだ発表していません。がんばってください!
|
 Z28 Z28  最短距離(円すいの側面) 最短距離(円すいの側面)
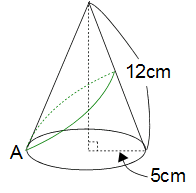
左の図のように、底面の半径が5cm、母線の長さが12cmの円すいがあります。点Aから円すいの側面を最も短い距離で1周し点Aに戻る曲線で側面を2つの部分に分けます。面積が大きい方は何cm2ですか?(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z27 Z27  軌跡(正三角形の回転移動) 軌跡(正三角形の回転移動)
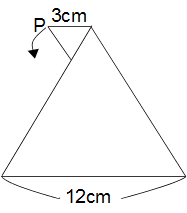
左の図のような1辺の長さが12cmの正三角形の周りを、1辺の長さが3cmの正三角形が矢印の方向にすべらないように1周してもとの位置に戻ります。このとき、点Pが動いてできる線の長さは何cmですか?(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z26 Z26  体積の割合(正四角すいの切断) 体積の割合(正四角すいの切断)
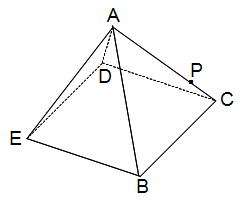 左の図のように、すべての辺の長さが等しく、高さが6cmの正四角すいABCDEがあります。 左の図のように、すべての辺の長さが等しく、高さが6cmの正四角すいABCDEがあります。
辺ACを4:1に分ける点をPとし、3点P、D、Eを通る平面で正四角すいを切断します。できた2つの立体のうち、小さい方の立体の体積は、正四角すいの体積の何倍ですか?
解答と解説 まだ発表していません。がんばってください!
|
 Z25 Z25  面積(重なる円) 面積(重なる円)
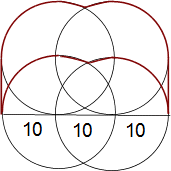
円の半径はすべて10cmです。茶色の線で囲んだ部分の面積は何cm2ですか?
解答と解説 まだ発表していません。がんばってください!
|
 Z24 Z24  面積(不思議な結果があります) 面積(不思議な結果があります)
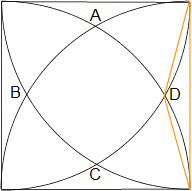
左の図のように、1辺の長さが12cmの正方形の中に4つのおうぎ形があります。オレンジ色の線で囲んだ三角形の面積は9.6cm2です。中央の図形ABCDの面積は何cm2ですか?(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z23 Z23  面積(円と三角形) 面積(円と三角形)
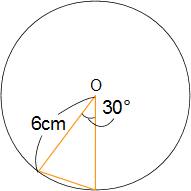
左の図のオレンジの線で囲んだ部分の面積は何cm2ですか?
Oは円の中心です。
解答と解説 まだ発表していません。がんばってください!
|
 Z22 Z22  立方体切断後の面の数 立方体切断後の面の数
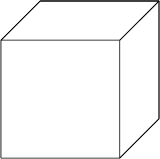
立方体を平面で切断して2つの立体に分けるとき、2つの立体の面の数の和は何面になりますか? 一番少ない場合と一番多い場合を答えてください。
解答と解説 まだ発表していません。がんばってください!
|
 Z21 Z21  面積(複合図形) 面積(複合図形)
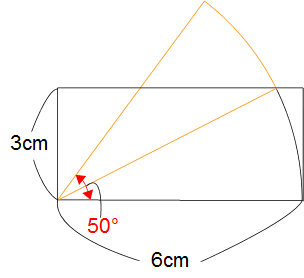
左の図は、タテが3cm、横が6cmの長方形と、半径6cm、中心角が50°のおうぎ形を組み合わせてできた図形です。オレンジ色の線で囲んだ部分の面積は何cm2ですか?(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z20 Z20  水面の高さ(円柱+円すい台) 水面の高さ(円柱+円すい台)
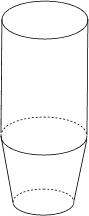
左の図のように「底面の半径が2cm、高さが6cmの円柱」と「底面の半径が2cm、高さが6cmの円すいを半分の高さで切り取った立体」を合わせた形のカプセルがあります。このカプセルに容積の半分だけ水を入れ、左の図のように立てて置くと水の高さは何cmになりますか?(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z19 Z19  面積(三角形の回転移動) 面積(三角形の回転移動)
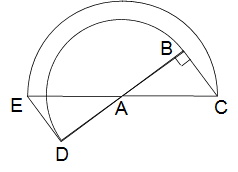
AB=12cm、BC=5cm、AC=13cmの直角三角形ABCがあります。直角三角形ABCを点Aのまわりに180°回転したら直角三角形ADEに移りました。
このときBCが動いた部分の面積は何cm2ですか?
(円周率 3.14)
解答と解説 まだ発表していません。がんばってください!
|
 Z18 Z18  面積(長さの比と面積の比) 面積(長さの比と面積の比)
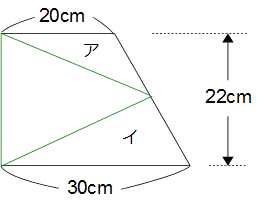
左の図は高さ22cmの台形です。三角形アの面積と三角形イの面積が4:5であるとき、緑の線で囲んだ三角形の面積は何cm2ですか?
解答と解説 まだ発表していません。がんばってください!
|
 Z17 Z17  体積(円すい台) 体積(円すい台)
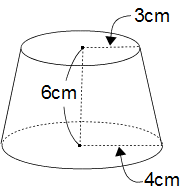
左の図のように、大きな円すいから小さな円すいを切り取った立体があります。上下の円の半径がそれぞれ3cm、4cmで、高さが6cmのとき、この立体の体積は何cm3ですか?(円周率 3.14)
解答と解説 こちら でご確認ください。
|
 Z16 Z16  面積(相似) 面積(相似)
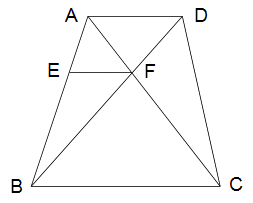 右の図で辺ADと辺BCと辺EFは平行です。 右の図で辺ADと辺BCと辺EFは平行です。
また、台形ABCDの面積は三角形ABCの面積の
1と2/3倍で、三角形AEFの面積は2と2/5cm2です。
辺ABをAの方に、辺CDをDの方にそれぞれまっすぐ
延ばした線が交わる点をGとするとき、
三角形GBCの面積は何cm2ですか?
解答と解説 こちら でご確認ください。
|
 Z15 Z15  面積(切り取り) 面積(切り取り)
正方形と直角三角形を組み合わせた図形を下の図のように一部を切り取ると、
アとイの部分の面積が等しくなりました。切り取った部分の面積は何cm2ですか?
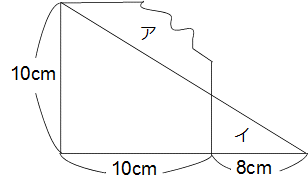
解答と解説 こちら でご確認ください。
|
 Z14 Z14  面積比(平行移動) 面積比(平行移動)
三角形ABCを辺BCの延長上に平行移動したとき、
ア、イ、ウの面積比を簡単な整数で表しなさい。
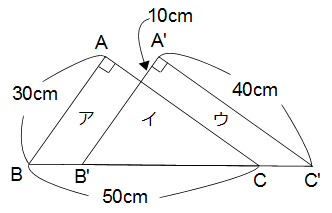
解答と解説 こちら でご確認ください。
|
 Z13 Z13  面積(直角二等辺三角形) 面積(直角二等辺三角形)
下の図のように直角二等辺三角形ABCの中に3つの直角二等辺三角形を作ります。
このとき緑色の線で囲んだ部分の面積は何cm2ですか?
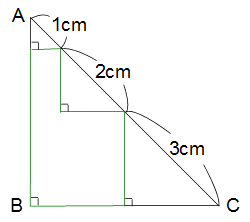
解答と解説 こちら でご確認ください。
|
 Z12 Z12  線分の長さ(相似) 線分の長さ(相似)
下の図のように直角三角形ABCと直角三角形DCBの斜辺(直角と向き合う辺)の交点を
Eとして、点EよりBCに垂直な線EFをひきます。
このときEFの長さを求めなさい。
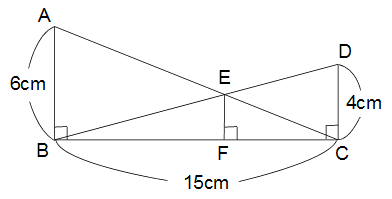
解答と解説
こちら でご確認ください。
|
 Z11 Z11  線分の長さ(合同と相似) 線分の長さ(合同と相似)
下の図のような長方形の紙があります。辺AB上に点Eをとり、CEを折り目にして折ると、
点Bはちょうど辺AD上にきました。
この点をFとするとAFの長さは2cmになりました。
BEの長さを求めなさい。
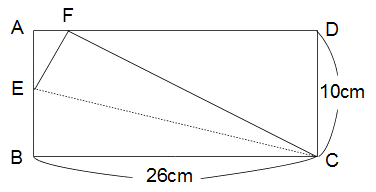
解答と解説
こちら でご確認ください。
|
 Z10 Z10  円の回転と軌跡 円の回転と軌跡
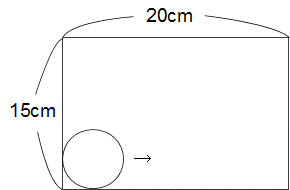
左の図はタテ15cm、横20cmの長方形です。
この長方形の内部を半径3cmの円が長方形の
辺に沿って1周したとき、円が通り過ぎる部分の
面積は何cm2ですか?(円周率 3.14)
解答と解説
こちら でご確認ください。
|
 Z09 Z09  面積(長方形とおうぎ形) 面積(長方形とおうぎ形)
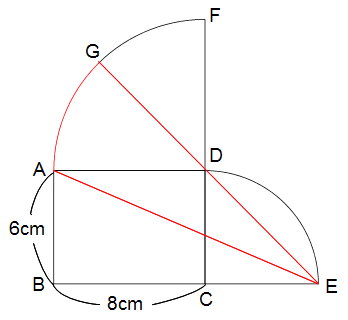
左の図は長方形ABCDに、ADおよびCDを
半径とする四分円(円の1/4)を
組み合わせたものです。いま、点AとEを
結び、2点D、Eを通る直線が弧と交わる点
をGとしたとき、赤い線で囲んだ図形AEGの
面積は何cm2ですか?(円周率 3.14)
解答と解説
こちら でご確認ください。
|
 Z08 Z08  面積の比(正三角形と円) 面積の比(正三角形と円)
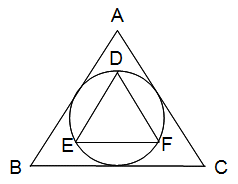
左の図のように大きな正三角形ABCにちょうどぴったり
入る円があり、その内側に円にちょうどぴったり入る
小さな正三角形DEFがあります。
このとき、2つの正三角形ABCとDEFの面積の比を
求めなさい。(円周率 3.14)
解答と解説 こちら でご確認ください。
|
 Z07 Z07  表面積(回転体) 表面積(回転体)
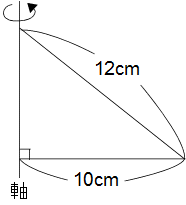
左の図のような三角形を軸のまわりに1回転させて
できる立体の表面積は何cm2ですか?(円周率 3.14)
解答と解説 こちら でご確認ください。
|
 Z06 Z06  体積(三角柱の切断) 体積(三角柱の切断)
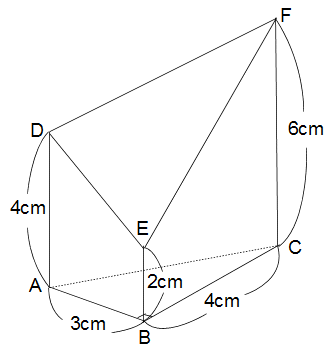
左の図は角ABCが90°、ABが3cm、
BCが4cmの三角形ABCを底面とする
三角柱を3点D、E、Fを通る平面で
斜めに切った立体です。
この立体の体積は何cm3ですか?
解答と解説
こちら でご確認ください。
|
 Z05 Z05  角度 角度
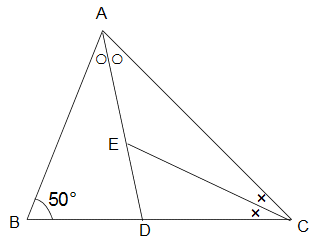
左の図のように三角形ABCで、
辺BC上に点Dを、AD上に点Eを角BADと
角CADが等しく、角ACEと角DCEが等しくなるようにとります。
角ABCが50°のとき、角CEDは何度ですか?
解答と解説
こちら でご確認ください。
|
 Z04 Z04  図形の構成 図形の構成
 面積5cm2の正方形のタイルを左の図のように 面積5cm2の正方形のタイルを左の図のように
タテ4個、横4個並べました。
図の中にある大小すべての正方形の面積の和は
何cm2ですか?
解答と解説 こちら でご確認ください。
|
 Z03 Z03  面積の比(相似) 面積の比(相似)
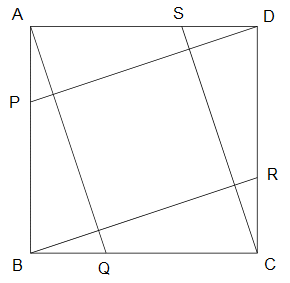
左の図の正方形のABCDで、
P、Q、R、Sは各辺を3等分した点です。
線分AQ、BR、CS、DPを引いたとき、
中央にできる正方形の面積は、正方形ABCDの
面積の何倍ですか?
解答と解説
こちら でご確認ください。
|
 Z02 Z02  面積(ひもの先端が動く) 面積(ひもの先端が動く)
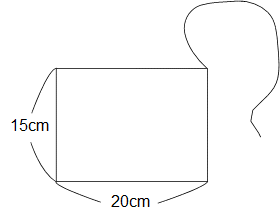
左の図のような長方形の1つの頂点にひもが
ついています。ひもの長さは30cmです。
ひもの先端が動ける部分の面積を求めなさい。
ただし、ひもは長方形の内部には入れません。
(円周率 3.14)
解答と解説
こちら でご確認ください。
|
 Z01 Z01  角度 角度
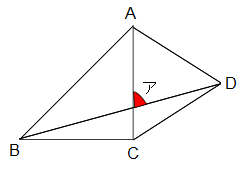
左の図は直角二等辺三角形ABCと正三角形ACDを
組み合わせた図形です。
角アの大きさは何度ですか?
解答と解説
こちら でご確認ください。
|

東京近郊で中学受験を目指すお子様への算数家庭教師はさんじゅつまんにお任せください。
下記リンク「中学受験算数家庭教師について」をお読みになり、そのページ内に設置してあるフォームよりご連絡ください。
|



