 |
 �Z���̕������Ă���ƌ��������邱�Ƃ�����Ǝv����p��W�ł��B�ŏ��͂��܂葝�₷������Ȃ��A�g�b�v�y�[�W�Ƀq�b�\���u���Ă������R�[�i�[�ł������A���������₵�Ă����v��𗧂āA���̃y�[�W�ɏ��i�����邱�Ƃɂ��܂����B���y���݂��������B �Z���̕������Ă���ƌ��������邱�Ƃ�����Ǝv����p��W�ł��B�ŏ��͂��܂葝�₷������Ȃ��A�g�b�v�y�[�W�Ƀq�b�\���u���Ă������R�[�i�[�ł������A���������₵�Ă����v��𗧂āA���̃y�[�W�ɏ��i�����邱�Ƃɂ��܂����B���y���݂��������B���u�b�����v�̐����ŁA�U�N���̏\���\��x��ߘa���N�x�̂U�N����ɒ����܂����B �����́u���v�艿�́u�āv�����́u�v���v�́u��v���Ȃ������t�B�������P�Ƃ��A�艿�A�����A���v�̏��Ɋ������߂Ă������̂悤�Ȗ����u���Ă�v�̖��ƌ����B �o��� ����i���Ɍ����̂Q���̗��v��������Œ艿���������A����Ȃ��̂Œ艿�̂P�������Ŕ������Ƃ���400�~�̗��v���������B���̕i���̌����͂����炩�H ��@ �������P�Ƃ���ƒ艿��1.2 ������1.2�~(1-0.1)��1.08 ���v��1.08-�P=0.08�ɂ����邩��A ���̕i���̌�����400��0.08��40000���W��5000�~(����) �����������Ƃ��ƁB ��Ꭾ�`�F�a���o�F�p�Ő��藧�����`�~�p���a�~�o�̎Z���炵���������@�B �u�����̐ςƊO���̐ς��������v�������Y��Ă��܂����k�ł��A ���̊o�����͖Y��Ȃ��炵��(����)(^-^) �ׂ傤����B���Ɓ������m�AA�AB�AP�AQ�����m�ŁA���̂Q�����������镶�͑�̂��ƁB ���{����P�@���@���̗�ł́��{����300 ���~A�|���~B��Q�@���@���̗�ł́��~20�|���~300��4400 �T�^�I�ȏo���Ƃ��Ď��̂悤�Ȗ�肪����A���̃X�g�[���[����ُ��Z�̖��O������B �o��� �S����300�̃R�b�v���^�Ԏd��������A�^�яI�����1�ɂ�20�~���炦�A���Ƃ��ĉĂ��܂���1�ɂ�300�~�ُ����Ȃ��Ă͂Ȃ�Ȃ��B���̎d���Ŏ�������z��4400�~�̂Ƃ��A�Ă��܂����R�b�v�͉��ł����H ��@ 300���ׂẴR�b�v���^�Ԃ�300�~20��6000�~���炦��͂��B���ۂɂ�������̂�4400�~������1600�~�s�����Ă���B�^�Ԃ��ƂƉ��Ƃł�1�ɂ�20�{300��320�~�̍������邩��A1600��320��5���A���R�b�v��5��(����) ���Ȃ݂��|�Ŏ����������Z�̕������{(�����Z)�ł���邩�ߎZ�ƌĂ�A���̈Ӗ��ŕُ��Z���邩�ߎZ�̈��Ƃ��ĕ��ނ��Ă���e�L�X�g��Q�l��������B ��ʂ��ω�������̊������A�ω�����O�̊�ʂɂ��낦�邱�ƁB �u1���ڂ��{�S�̂̃y�[�W��20����ǂ݁A2���ڂ��c��̃y�[�W��15����ǂނ�340�y�[�W�c�����v�Ƃ������ł́A1���ڂ�2���ڂŊ����̊�ʂ��ω����Ă���B��2�����̑������� ���������ꍇ�A2���ڂ̊�����1���ڂ̊����Ɠ����悤�ɁA�{�S�̂ɑ��銄���ɂ��낦�čl����Ƃ킩��₷���B (1�|0.2)�~0.15��0.8�~0.15��0.12 [12��]�c2���ڂ̖{�S�̂ɑ��銄�� �{�S�̂̃y�[�W�����߂�Ȃ�A340��(0.8�|0.12)��340��0.68��500�y�[�W�B 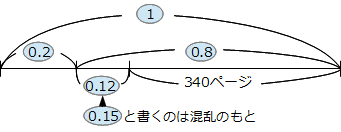 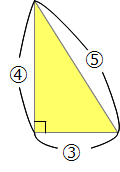 ����������B���p�O�p�`�̂R�ӂ̒����̔䂪�A�אڂ���������������ɂȂ�`�Ƃ��ėL���B�Q�ӂ̒������킩���Ă����(��^9cm:12cm=�B:�C)�A�c��P�ӂ̒���(�D=15cm)�̎Z�o���e�ՁB�������A3:4:5�̒m�����������ɂ��������Z�o���s���̂�(�Z���ł�)�����e�Ղł͂Ȃ��B ����������B���p�O�p�`�̂R�ӂ̒����̔䂪�A�אڂ���������������ɂȂ�`�Ƃ��ėL���B�Q�ӂ̒������킩���Ă����(��^9cm:12cm=�B:�C)�A�c��P�ӂ̒���(�D=15cm)�̎Z�o���e�ՁB�������A3:4:5�̒m�����������ɂ��������Z�o���s���̂�(�Z���ł�)�����e�Ղł͂Ȃ��B���ۂ̓����ł͂��̒m����O��Ƃ����o����Ȃ���Ă���A����͏o��҂̎Z���̌������Ⴂ�Ƃ������邪�A���Ƃ��Ă͊o���Ă��đ��͂Ȃ��B���Ȃ݂Ɏ��Ă�����̂Ƃ���5:12:13�A8:15:17�Ȃǂ�����B ���ڂ����͒��w���w�́u�O�����̒藝�v�Ŋw�K���܂��B�O�����̒藝�ɂ��Ă͎Z���ŏؖ����ł��܂����A�������ł͂��������w�i�⍪�����܂������l�������A�P��3:4:5��m���Ƃ��ėv�����Ă��邱�Ƃ�����܂��B  5.5���͎��v�Z�ɕp�o����p�x�B 5.5���͎��v�Z�ɕp�o����p�x�B�u8����Ŏ��v�̒��j�ƒZ�j���d�Ȃ鎞���v�́A���j��8�����傤�ǂ̎��_��240���O�����Z�j�ɒǂ����܂ł̎��Ԃ��l����B���̂Ƃ����j�̑���������6���A�Z�j�̑���������0.5���ł��邱�Ƃ���A���j�͒Z�j�ɑ���1���Ԃ�5.5��(��6�|0.5)���ǂ������ƂɂȂ�B8����ŏd�Ȃ鎞���́A240��5.5��240/5.5��480/11��8��43��7/11(��) ����x�̍������ł́A�����̘a6.5�����p�����邱�Ƃ�����B ���w���҂ɂ���Ă�5.5�ɑウ�ĕ���11/2���g���P�[�X������Ǝv���܂����A�{�N�͂ӂ���5.5�̗��p�𐄏����Ă��܂��B��̌v�Z���@�����Q�l���������B��x�����5.5������܂����A���ꕪ�q���Q�{����Ƃ����ɏ����ĂȂ��Ȃ�܂�(^^)/ 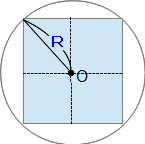 �}�̂悤�ɁA�~�Ƃ��̉~�ɓ��ڂ��鐳���`������Ƃ��A�����`�̖ʐς��킩���Ă��Ă��A���ꂪ��قnjb�܂ꂽ���l�ł���ꍇ�������A�~�̔��a�����߂邱�Ƃ��ł��Ȃ��͎̂Z���̒�ԁB �}�̂悤�ɁA�~�Ƃ��̉~�ɓ��ڂ��鐳���`������Ƃ��A�����`�̖ʐς��킩���Ă��Ă��A���ꂪ��قnjb�܂ꂽ���l�ł���ꍇ�������A�~�̔��a�����߂邱�Ƃ��ł��Ȃ��͎̂Z���̒�ԁB���Ƃ��ΐ}�ɔ����u���[�Ŏ����������`�̖ʐς�36cm2�̂Ƃ��A������S�������������`�̖ʐς�9cm2������A�����`�̖ʐς̌���[�Ίp���~�Ίp����2]���g���A�q�~�q��2��9���A�q�~�q��18�Ƌ��߂邱�Ƃ͉\�B�������Z���ɂ̓��[�g�̊T�O���Ȃ�����A�q���̂̐��l�����߂邱�Ƃ͂ł��Ȃ��B �����[�g�̒m��(���ȏȂ̕W���J���L�������ł͒�3�ŗ��C)������Ȃ�q����18��3��2 ���q�~�q��18�Ƃ������ɂ͂q���Q���邱�Ƃ���A�q��18���Q���X�Ɗ��Ⴂ���鐶�k�������̂Œ��ӂ��K�v�B �q���̂̐��l�͋��߂��Ȃ��Ă��A�q�~�q��18�̏����A�~�̖ʐς����߂邱�ƂɎx��͂Ȃ��B�~�̖ʐρ����a�~���a�~3.14���q�~�q�~3.14��18�~3.14��56.52cm2�Ƃ����v�́B ���Ђ̂�B �`�F�a�ł���Q�̗ʂ�����A���̑o���ɓ������`�F�a�̗ʂ��������Ƃ�(�܂��͑o������`�F�a�̗ʂ��������Ƃ�)�A���̘a(��)�ɂ����Ă��`�F�a�̔䂪�ێ�����闝���̂��ƁB ���Ƃ���600g��400g�A120g��80g�̔�͂ǂ����3:2�ŁA���҂̘a720g(=600+120)��480g(=400+80)�̔��3:2�ɂȂ��Ă���B 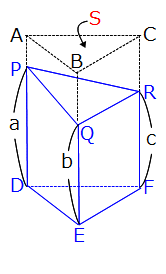 ����Ƃ��������イ�B ���}�̂悤�ɁA�O�p��ABC-DEF���Ζ�PQR�Őؒf��������PQR-DEF�̂��ƁB�O�p���̓����f���ꂽ(�ؒf���ꂽ)���Ƃ��炱�̖��܂�������B �f���O�p��PQR-DEF�̑̐ς� �m���Ƃ̎O�p���̒�ʐ�S�n�~�ma�Ab�Ac �̕��ϒl�n�ŋ��߂���B �Ȃ��A���}�̒f���O�p���́A�㑤�̎Ζʂ����ɂ��ؒf�����A���킹�ĉ�����ؒf����f���O�p��������(�e���g�^�Ȃ�)�B �����܂�߂ĊT��(���悻�̐�)�����Ƃ��̕��@�̈�B �ʏ�A��蕶�ɂ́u���̈ʂŐ�グ�ĊT���ɂ���v�܂��́u��グ�����̈ʂ܂ł̊T���ɂ���v�Ƃ����ǂ��炩�̎w��������B���̂Q�͓����Ӗ��̎w���B ���̈ʂŐ�グ�ĊT���ɂ���(����グ�����̈ʂ܂ł̊T���ɂ���) ���̈ʂ��܂߁A����ȉ��̐����͂��ׂĂO�Ƃ��A���̈ʂ̐����Ɋւ�炸�A�P��ʂ����̈ʂ̐������P���₷�B �������A���ȉ��̈ʂɂ܂����������Ȃ��ꍇ(���ׂĂ̈ʂ̐������O�̏ꍇ)�����̐����͑����Ȃ��B ���Ƃ�����̈��Ő�グ��30000�ɂȂ鐮���͈̔͂�20001�ȏ�B�����20000�ȏ�Ɠ�����듚�ɒ��ӁI  �E�}�̂悤�ɂ��Ȃǂ��ЂƂ܂�肸���ׂĂ����ƁA�ʏ�ЂƂ܂������̌��͂W���Ȃ��Ȃ�B�������A�ЂƂ܂�肪�W�ɂȂ����ꍇ�����͗�O�ŁA����ɓ����ɂP�u�����Ƃ��ł���B �E�}�̂悤�ɂ��Ȃǂ��ЂƂ܂�肸���ׂĂ����ƁA�ʏ�ЂƂ܂������̌��͂W���Ȃ��Ȃ�B�������A�ЂƂ܂�肪�W�ɂȂ����ꍇ�����͗�O�ŁA����ɓ����ɂP�u�����Ƃ��ł���B��O��1�������ЂƂ܂��̌��͂S�̔{���ŁA�O������̌�����͎��̂Q�p�^�[�����l������B�����͉E�}�̏B �E�c�c��48��40��32��24��16���W���P(��O) �E�c�c��44��36��28��20��12���S(��O�i�V) 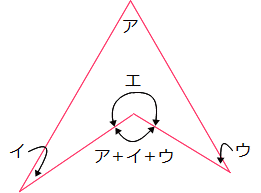 �E�}�̂悤�Ȏl�p�`�̎Z���I���́B�������͉̂�(����)�l�p�`�B���l�p�`���ʏ�̎l�p�`���l�A���p�̘a(�A�{�C�{�E�{�G)��360���ɂȂ�B�A�{�C�{�E�̘a���A�G�ƌ��������p�Ɠ������Ȃ鐫���͗L���B�C�ƃE���Ȃ��A�C�G����������Ȃǂ��낢��Ȋm�F���@������̂Œ��ׂĂ݂Ă��������B �E�}�̂悤�Ȏl�p�`�̎Z���I���́B�������͉̂�(����)�l�p�`�B���l�p�`���ʏ�̎l�p�`���l�A���p�̘a(�A�{�C�{�E�{�G)��360���ɂȂ�B�A�{�C�{�E�̘a���A�G�ƌ��������p�Ɠ������Ȃ鐫���͗L���B�C�ƃE���Ȃ��A�C�G����������Ȃǂ��낢��Ȋm�F���@������̂Œ��ׂĂ݂Ă��������B3�F5�̋t��͐�������ꂩ����5�F3�Ƃ���悢���A2�F3�F4�̂悤��3��(�ȏ�)�̔�̋t���4�F3�F2�Ƃ͂Ȃ�Ȃ��B�R��(�ȏ�)�̔�̋t��͊e���̋t�������A����̍ŏ����{���������Đ�������B 2�F3�F4�̋t�䁨1/2�F1/3�F1/4��6�F4�F3 (12�{����) �������ɂ��B �Q�̐������P�ȊO�̌��������Ȃ��W�̂��ƁB �Q�̐������Ƃ��ɑf���ł���Γ��R�݂��ɑf�ł��邪(��^3��7�݂͌��ɑf)�A�K�������f���ł���K�v�͂Ȃ��B��^9(��3�~3)��20(=2�~2�~5)�ɂ͂P�ȊO�̌����Ȃ��݂��ɑf�B [�Z���ł̎g�p��] 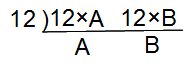 �ő����12�A�ŏ����{����144�ł���2�̐��������߂Ȃ����B �ő����12�A�ŏ����{����144�ł���2�̐��������߂Ȃ����B�c�c2�̐�����12�~A�A12�~B(A>B�AA��B���݂��ɑf)�Ƃ���ƁA �ŏ����{���͉E�̘A���@�ŊO�����ׂĂ̐ς�����12�~A�~B��144 �����A�~B��12 A>B���AA��B���݂��ɑf�ł���(A�AB)�̑g�̓A(12�A1)�ƃC(4�A3) ���߂�2�̐����́A �A���@12�~A=12�~12��144�@�Ɓ@12�~B=12�~1=12 �C���@12�~A=12�~4��48�@�Ɓ@12�~B=12�~3=36 ���@(A,B)��(144,12)�܂���(48,36) ������A=6�AB=2��I��ł��܂��ƁA6��2�݂͌��ɑf�ł͂Ȃ�����(����2������)�A�ő����12�ł͂Ȃ�24(=12�~2)�ɂȂ��Ă��܂��B �����Ԃ��B 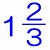 (1��3����2)�悤�ɐ������������镪���̂��ƁB�����ƕ����̐ڑ����̓ǂ݂́u���v�B (1��3����2)�悤�ɐ������������镪���̂��ƁB�����ƕ����̐ڑ����̓ǂ݂́u���v�B���\�N�قǑO�܂ł́u���v�Ɠǂ�ł����B�����������₨�������ɕ����Ă݂悤�I �ѕ����͉������ɒ������Ƃ��ł��A��̑ѕ����u1��3����2�v�͉������u3����5�v�Ɠ������B ���������c���Ԃ��B���q��������傫�����A���q�ƕ��ꂪ���������� �ʏ�A�Z���̊w�K�ł́u�͉������ɂ����A�ѕ����ɒ����ĉ���v�����������A���w��������m�̖͋[�����ł͉������̉����e���邱�Ƃ������B���������ׂĂ̓��w�����ŋ��e�����ۏ͂Ȃ��̂ŁA�O�̂��ߑѕ����ɒ����Ă����ق������S�^�]�B�Ȃ��A�ѕ����͎Z�������Ŏg���閽�̒Z�������ŁA���w�ȍ~�̐��w����͂��̎p�������B �������̈قȂ鑬���Ői�s���ɂ��� �g�[�^���̏��v���Ԃ�ς����ɁA���̑����Ői�ƍl����ꍇ�̑����̂��ƁB ���Ƃ���300m���ꂽ2�n�_�Ԃ����H-����50m�A���H-����30m�ʼn�������ƁA ���v���Ԃ�300��50�{300��30��6�{10��16���ŁA ���ς̑�����(300�~2)��16��600��16������37.5m�B ���̂悤�ɁA�����̕��ς̑��������H�ƕ��H�̒P���ȑ�������(50�{30)��2��40�ɂ͂Ȃ�Ȃ��B ���H�̑�����A�A���H�̑�����B�Ƃ����Ƃ��A ���ς̑�����(A�~B�~2)��(A�{B)�Ƃ�������������B���ς�2�{��a�Ŋ��� �}�C�i�X�̐����Ȃ����Ƃɂ���Đ�����Z���Ɠ��̐������@�B���Ƃ��A�w�Z�̎n�Ǝ��Ԃɑ��āu12�������������Ɓv�Ɓu8���x��邱�Ɓv�̍���12+8=20���B12�|(�|8)��20�ƍl����Έ����Z�̍��ł��邪�A�Z���ɂ̓}�C�i�X�̐����Ȃ�����A���Ό�̍��������ċ��߂��Ǝw������B�u����10L�̋����v�Ɓu����5L�̔r���v�̍���10+5=15L�ɂȂ�̂����l�B ���͑�̒��ŁA�`�a�b�Ɠ����悤�ɐl��ꏊ�A���etc�̖��܂��Ƃ��čb�A���A���̏��Ԃɗp�����邱�Ƃ�����B�{���͌×���������`������\��(��������)�ƌĂ�A�b��������ȍM�h�p�(�����E���E�ւ��E�Ă��E�ځE���E�����E����E����E��)�̏��B�������\��x�Ƒg�ݍ��킹�A10��12�̍ŏ����{���Z�\�N�łЂƉ��(�җ�)������\���\��x�͗L���B�֑��Ȃ���A������܂�͉��{��(�ݔN)������(���̂Ƃ�)�B���݂̘Z�N���͕���19�N4���`12�����܂�Ȃ璚�{��(���̂����N)������(�Ђ̂Ƃ�)�A����20�N1���`3���̑����܂�Ȃ��+�q(�˂��ݔN)����q(���̂���)�B�Z���ł͍b�����܂ł̒m���ŏ\���ł��B ���Z�N���Ƃ�2019�N�x(�ߘa���N�N�x)�̘Z�N���ł��B �������v�̕��͑�ŁA�艿��l�������Ĕ���Ƃ��̒l�i�̂��ƁB����(�o�C�J)�Ƃ������B��ʂɂ͒l�����������ɒ艿�Ŕ���Β艿���̂��̂�����l�ƂȂ邪�A�Z���ł͂��̏ꍇ�͔���l�Ƃ͌ĂȂ��B����l�͂����܂ł��l������̒l�i�B �Z���Ɠ��̍l�����ŁA�u���v�̂��Ƃ��u�H���̗n���Ă��Ȃ��H�����v�ˁu0%�̐H�����v�Ƒ�����ꍇ������(��R�u���Q��)�B�O�p�`�����0�̑�`�Ƒ������肷��̂�����Ɏ��Ă���B �b����m��������km�Ɋ��Z����Ƃ��̌v�Z�B3600�{����1000�Ŋ��邱�Ƃ��܂Ƃ߂����́B�t�Ɂ������Ɋ��Z����Ȃ�3.6�Ŋ���悢�B  �W���̗v�f�̌�������}�\�̂��ƁB�Z���ł́A�Q�̃A���P�[�g�ɂ��ꂼ��Q�̉������肪�p�o�B�����������ɂ͂S�}�X(2�~2)�̃J���m�[�}�𗘗p����ƃx���}���ȒP�Ȃ��Ƃ������B �W���̗v�f�̌�������}�\�̂��ƁB�Z���ł́A�Q�̃A���P�[�g�ɂ��ꂼ��Q�̉������肪�p�o�B�����������ɂ͂S�}�X(2�~2)�̃J���m�[�}�𗘗p����ƃx���}���ȒP�Ȃ��Ƃ������B�̔��Ό�B�����̕��q�ƕ���{���邱�ƁB�������̂̑傫���͕ς��Ȃ��B1/2��5/10�ȂǁB�͗L���Ȃ̂ł����A�{���͂��܂�m���Ă��Ȃ��悤�ł��B ����ȏ���邱�Ƃ��ł��Ȃ������̂��ƁB����́u���v�͌P�ǂ݂Łu����(��)�v�B�܂�A���łɖ���Ă��镪���B  �����̂R�������o����Ƃ��̌�C���킹�B�^�e�̌v�Z�͊���Z�A���R�̌v�Z�͂����Z�B����聁���₳�~������ �̂悤�Ɏg���B�������̂Ƃ��āA�H�����̌�C���킹�u�������v�Ȃǂ�����B �����̂R�������o����Ƃ��̌�C���킹�B�^�e�̌v�Z�͊���Z�A���R�̌v�Z�͂����Z�B����聁���₳�~������ �̂悤�Ɏg���B�������̂Ƃ��āA�H�����̌�C���킹�u�������v�Ȃǂ�����B |
�����ߍx�Œ��w��ڎw�����q�l�ւ̎Z���ƒ닳�t�͂���܂�ɂ��C�����������B ����]�̕��́A���L�����N�u���w�Z���ƒ닳�t�ɂ��āv�����ǂ݂ɂȂ�A���̃y�[�W���ɐݒu���Ă���t�H�[����育�A�����������B���O�̂��₢���킹�����}�ł��B |