今回の第３講座では〈食塩水問題のはやわざ〉を紹介しようと思います。
俗にてんびんと呼ばれている解法で、これを身につければ、今まで食塩水問題で苦しんでいた人も、その苦労からだいぶ解放されることでしょう。


初めに〈食塩水の３公式〉を確認しておきます。てんびんを使って食塩水の問題を解くとき、
３公式は使わずに済んでしまうことも多いのですが、やはり３公式は覚えておくべきでしょう。

食塩水の３公式
食塩の重さ＝濃さ×食塩水の重さ　　　し＝こ×水
濃度＝食塩の重さ÷食塩水の重さ　　　こ＝し÷水
食塩水の重さ＝食塩の重さ÷濃さ　　　水＝し÷こ

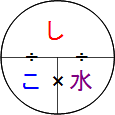
　しは塩、こは濃さ、水（すい）は食塩水
　左のように「しこすい」と覚えておくと忘れないかな。
　タテは割り算、ヨコはかけ算です。


ではここから てんびん の説明に入ります。
てんびんは次のような食塩水を混ぜる問題で大きな力を発揮します。

20％の食塩水の重さ、さらにでき上がる12％の食塩水の重さがわかっていませんから、ごく普通に３公式を使って解くのは難しそうです。　そこで…。

ボクがソフトで作った図版なのですが、これが噂（うわさ）のてんびんです。
さっそく使い方を解説しましょう。

手順１　てんびんのウデの両端に、混ぜる食塩水の濃さを記入します。
　　　　　 ※濃さがうすい方を左端、濃い方を右端に書くと見やすいですよ。

手順２　支点の上に、混ぜてできる食塩水の濃さを記入します。

手順３　ぶらさがっているおもりのところに、それぞれの食塩水を混ぜる重さを記入します。

すべての箇所の数がわかっていれば問題になりませんから、
手順１〜手順３のどこかで、数が書けないところがあるはずです。

では実際に、上の問題の数値を記入してみましょう。



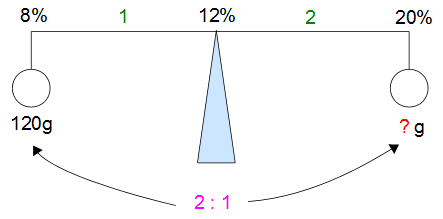
20％の食塩水の重さがわからないから、そこは？ｇとしてあります。
ここからが具体的な計算方法です。

てんびんでは、
支点から両端までの長さと、下にぶらさがっているおもりの重さが逆の比になります。

この問題の場合、
（12−８）：（20−12）＝４：８＝１：２　→支点から両端までの長さの比
この比を逆にして、おもりの重さは２：１です。
２にあたる重さが120（g）だから、１にあたる重さは60（g）
これで20％の食塩水を混ぜる重さが60gであることがわかりました。

どうですか？　すごく簡単でしょう？　てんびんに圧倒されて、食塩水の３公式は出てくる暇もありませんでした。

ついでに左右のウデの長さと、その下のおもりの重さの積が一致するという確認方法も知っておくと便利でしょう。上の問題では（12−8）×120と（20−12）×60が等しくなります。

さらに大切な補足をすると、
混ぜるものが食塩水ではなく、食塩や水であってもてんびんの利用は可能です。
その場合は、濃さの部分を次のように書いてください。
食塩を混ぜるとき→食塩を「水のない食塩水」と考え、濃さを100％と書く
水を混ぜるとき　→水を「食塩のない食塩水」と考え、濃さを０％と書く

＊＊＊
今回説明したてんびんを使うと、だいぶ広い範囲で食塩水問題と戦えると思います。もちろんてんびんが使えない意地悪な食塩水問題もあるんですけどね。
それについてはまたいつかお話ししますけど、かなり多くの問題で大丈夫なはずですから、みなさん、てんびんが使えそうな食塩水問題では、どんどん使っててんびん名人を目指してくださいね。