 Ｂ２０  売買損益
あるフルーツショップでパパイヤを300個仕入れ、2割5分の利益を見込んで定価をつけました。もし300個すべてを定価の1割6分引きで売っても、１個につき34円の利益があるそうです。ある日曜日、この300個のマンゴを定価で売り始めたところ、何個か売れましたが、売れ残りが出てしまったので、次の月曜日に定価の1割6分引きで売ったところ、すべて売り切れました。300個すべての利益を合わせると26520円になりました。日曜日に定価で売れたパパイヤは何個ですか？
解答 120個
解説 １個あたりの仕入れ値を１とすると定価は1.25で、定価の１割６分引きの売り値は1.25×（１－0.16）＝1.05です。定価の１割６分引きで売ったときの利益は1.05－１＝0.05で、これが34円にあたるから、仕入れ値１＝34円÷0.05＝680円と求めることができます。
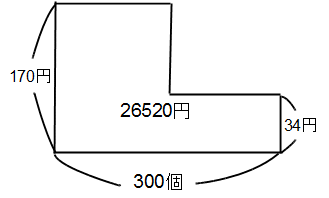 定価で売ったときの利益（１個あたり）は680円×0.25＝170円、定価の１割６分引きで売ったときの利益（１個あたり）は34円であり、これらを合わせて300個売ったときの利益の合計が26520円だから、左のような面積図を書いてつるかめ算を解くと、
26520－34×300＝16320（左上の長方形の面積）
16320÷（170－34）＝120（左側長方形のヨコの長さ） ここで求めた120個が定価で売ったパパイヤの個数です。
（１割６分引きで売った個数は300－120＝180個です）
※つるかめ算の面積図、ご存知でしたでしょうか？ ダイレクトにつるかめ算だけで済む入試問題は減っていますが、問題を解く過程では活躍することが多いです。覚えてくださいね！
|
Ｂ１９ 相当算
Ａ君、Ｂ君、Ｃ君の３人が湖に釣りに行きました。Ａ君、Ｂ君の釣った魚の数の比は２：３でしたが、釣った魚のうち、Ａ君は16匹、Ｂ君は19匹を湖に放しました。Ｃ君は釣った魚の1/3を湖に放したので、Ａ君とＣ君の持ち帰った魚の数は同じになりました。また、３人が持ち帰った魚の数の合計は152匹でした。Ｃ君が釣った魚は何匹でしたか？
解答 63匹
解説
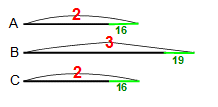 Ａ君が釣った魚を２、Ｂ君が釣った魚を３とします。Ａ君が持ち帰った魚は２より16匹少なく、Ｂ君が持ち帰った魚は３より19匹少なく、Ｃ君が持ち帰った魚はＡ君と同じです。３人が持ち帰った魚の合計は７（＝２＋３＋２）から51匹（＝16＋19＋16）を引いた{７－51}匹となり、これが152匹にあたります。
※左図は持ち帰った魚
７＝152＋51＝203匹より、１＝203÷７＝29匹。Ｃ君が持ち帰った魚は29×２－16＝42匹で、Ｃ君が釣った魚は42÷2/3＝63匹です。
※Ｃ君は釣った魚の1/3を放したから、持ち帰った魚は釣った魚の2/3倍です。
|
Ｂ１８ 仕事算（休みあり）
ある仕事を仕上げるのに、Ａ君だけですると32日、Ｂ君だけですると48日、Ｃ君だけですると96日かかります。この仕事をＡ君、Ｂ君、Ｃ君の３人でやり始めましたが、途中でＢ君が３日、Ｃ君が６日、病気で休んでしまいました。この仕事を終えるのに全部で何日かかりましたか？
解答 18日
解説 11/24thu分に続き、この問題も仕事の総量に自由な数が設定できる問題です。
 仕事の総量を32日、48日、96日の最小公倍数で96とします。
１日あたりの仕事量はＡ＝96÷32日＝３、Ｂ＝96÷48日＝２、Ｃ＝96÷96＝１です。
もし誰も休まずに仕事をすれば、１日に３＋２＋１＝６の仕事ができるから、すべての仕事が終わる日数は96÷６＝16日です。（図上）
実際にはＢが３日、Ｃが６日休んでいるから、休んで行われなかった分を加えて仕事の総量と考えることになります。（図下参照。休みが赤い数字。休みを除いた黒い数字の合計が96です。日数を求めるには休んだ仕事量を加える必要がありますね）
Ｂが３日、Ｃが６日休んだ分の仕事量は２×３＋１×６＝12
よって仕事を終えるのにかかった日数は（96＋12）÷６＝18日と求められます。
|
Ｂ１７ 条件整理
40人をＡ、Ｂ、Ｃ、Ｄ、Ｅの５つの班に分けました。班の人数は、Ａ班がＣ班より１人少なく、Ｄ班がＢ班より１人多く、Ｄ班とＥ班を合わせるとＡ班と同じになります。Ｃ班の人数は何人と考えられますか？考えられる人数をすべて求めてください。ただし、１人もいない班はないものとします。
解答 12人、13人
解説 問題の条件を下のような線分図で示しました。黒い線の合計が40人です。（赤い破線は40人にふくみません）
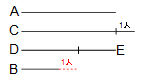 さて、Ａ班を13人以上にすることはできません。理由はＡ班を13人とすると、ＡＣＤＥ班で13×３＋１＝40人になってしまい、Ｂ班の人数がなくなってしまうからです。
Ａ班を12人とすると、ＡＣＤＥ班で12×３＋１＝37人。Ｂ班＝40－37＝３人になり、Ｄ班＝３＋１＝４人、Ｅ班＝12－４＝８人となって、すべての条件が満たされます。
Ａ班を11人とすると、ＡＣＤＥ班で11×３＋１＝34人。Ｂ班＝40－34＝６人になり、Ｄ班＝６＋１＝７人、Ｅ班＝11－７＝４人となって、すべての条件が満たされます。
Ａ班の人数を10人とすると、ＡＣＤＥ班で10×３＋１＝31人。Ｂ班＝40－31＝９人になりますが、Ｄ班＝９＋１＝10人である必要があり、この場合はＥ班の人数がなくなってしまいます。以下、Ａ班の人数が９人以下の場合も同様に条件を満たすことができません。求めるのはＣ班の人数だから、Ａ班の人数に１を加え、13人または12人が正解となります。
|
Ｂ１６ 旅人算（追いかけ）
グラウンドのまわりをＡ、Ｂ、Ｃの３人が同じ方向にそれぞれが一定の速さで何周か走ったところ、ＡはＢに４分ごと、Ｃに３分ごとに追いこされました。では、ＢはＣに何分ごとに追いこされましたか？
解答 12分
解説 この問題はみんなの算数講座第77講座で説明した、自由な数が用意できる問題です。
いま、グラウンドのまわりの長さを12に決めると（追いつくまでの時間）＝（１周の距離）÷（速さの差）を利用して、12÷（Ｂの速さ－Ａの速さ）＝４(分)…ア 12÷（Ｃの速さ－Ａの速さ）＝３(分)…イ という２つの式を作ることができます。アより（Ｂの速さ－Ａの速さ）＝12÷４＝３ イより（Ｃの速さ－Ａの速さ）＝12÷３＝４だから、Ｃの速さとＢの速さの差は４－３＝１であることがわかります。したがってＣがＢに追いつくまでの時間を12÷１＝12（分）と求めることができます。
※算数に慣れていないと、違和感を覚える解説だったかも知れません。中学生で方程式を勉強しますが、そのことが算数向きの柔軟な発想を妨げてしまうことは、どうやらこうした問題から明らかなようです。ぜひ算数的な発想にも親しんでいただきたいと思います。
|
Ｂ１５ のべ量
サンジュツドームで、ある韓流歌手のコンサートが４回行われました。入場者は４回で、のべ52000人でした。このうちコンサートに２回行った人は１回行った人の半分で、３回行った人は２回行った人の半分で、４回行った人は３回行った人の半分でした。少なくとも１回コンサートへ行った人*は何人ですか？
*２回行った人も１人とするように、何回かの来場を重複させない人数
解答 30000人
解説 １回行った人の半分が２回行った人、その半分が３回行った人、その半分が４回行った人だから、これを整数の比で表すと（１回の人）：（２回の人）：（３回の人）：（４回の人）＝８：４：２：１となります。のべ入場者とは、同じ人が何回入場しても別に数える人数のことで、上の比に回数をかけて合計した26（８×１＋４×２＋２×３＋１×４）が52000人にあたることがわかります。26＝52000人より１＝2000人。同じ人の入場を１回しか数えなければ、入場者は８＋４＋２＋１＝15だから、解答は2000人×15＝30000人と求めることができます。
|
Ｂ１４ 循環（じゅんかん）小数
１３／９９＋１３／９９９を小数で表すと、小数第１位から第50位までに４が何個あるでしょうか？
解答 17個
解説 0.777…など１ケタが繰り返す小数は7/9、0.525252…など２ケタが繰り返す小数は52/99、0.268268…など３ケタが繰り返す小数は268/999といった要領で、繰り返し部分を分子に、繰り返し部分と同じ個数の９を分母に並べることで、繰り返しの小数（循環小数）を分数に直すことができます。
このことを逆に利用すると 13/99＝0.131313…、13/999＝013/999＝0.013013…のように繰り返しの小数で表すことができます。これらの和は0.131313…＋0.013013…＝0.144326…となり、小数点以下（144326）の６ケタが繰り返します。
50÷６＝８余り２→小数第50位までに（144326）の繰り返しが８セットあり、（14）の２つが余る
したがって、小数第50位までの4の個数は２×８＋１＝17個と求めることができます。
※最後の式ですが、１セットに数字4が２個ずつ。さらに余り２つのうち１つが数字4ですね。
|
Ｂ１３ 組合せ
３ｃｍ、４ｃｍ、５ｃｍ、６ｃｍ、７ｃｍの５本の針金（はりがね）があります。この中から３本を選び、それらを辺とする三角形を作ります。全部で何通りの三角形を作ることができますか？
解答 ９通り
解説 ５個の異なるモノの中から３個を選ぶ組合せの数は ５C３＝５×４×３÷（３×２×１）＝10通りです。※組合せの計算方法については みんなの算数講座第14講 をご参照ください。
つまり、３ｃｍ、４ｃｍ、５ｃｍ、６ｃｍ、７ｃｍの５本の針金から３本を選ぶ方法は10通りあるのですが、じつは三角形の３つの辺は（最大辺の長さ）＜（残り２辺の長さの和）という条件を満たす必要があり、３ｃｍ、４ｃｍ、７ｃｍの針金を選んだ場合は三角形を作ることができません。短い２辺の３ｃｍと４ｃｍを加えても最大辺の７ｃｍを超えないからです。したがって解答は10通りから１通りを除外して９通りとなります。
|
Ｂ１２ 比の文章題
現在、長女、次女、三女の年令の比は４：３：１で、この３人の年令の和を２倍すると母親の年令になります。８年後には、３姉妹の年令の和がちょうど母親の年令と同じになります。現在の長女の年令は何才ですか？
解答 ８才
解説 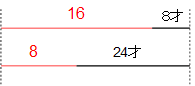 現在の三姉妹の年令を長女４、次女３、三女１とすると、母の年令は（４＋３＋１）×２＝８×２＝16です。８年後を考えると、三姉妹の年令の和は３人分で８×３＝24才増え、母の年令は（１人だから）８才増えます。これらが等しくなることから、左のような線分図をイメージすると、16と８の差が24才と８才の差にあたることがわかります。８＝16才より、１＝２才。したがって現在の長女の年令は２才×４＝８才となります。
※このような線分図のイメージで、比と具体的な数量を一致させるのは、算数ではじょうとう手段ですね。
|
Ｂ１１ 比の文章題
ミーちゃんの所持金とケイちゃんの所持金の比は５：３になっています。いま、同じ日からミーちゃんは毎日600円ずつ、ケイちゃんは毎日400円ずつ使ったところ、ミーちゃんが使い切る10日前に、ケイちゃんは使い切っていました。ミーちゃんとケイちゃんのはじめの所持金はそれぞれいくらでしたか？
解答 ミーちゃん60000円、ケイちゃん36000円
解説 600円と400円を比に直すと600：400＝３：２だから、仮に二人の初めの所持金が３：２であれば、お金は同じ日になくなるはずです。（加比の理という。／初めの所持金を３：２の金額に設定して調べてみてください）
〔仮定〕二人の初めの所持金３：２ ⇒同じ日にお金がなくなる
〔実際〕二人の初めの所持金５：３ ⇒ミーちゃんが10日間よぶんに使える
いま、２つの比でケイちゃんを６にそろえてみると、
〔仮定〕二人の初めの所持金３：２＝９：６ ⇒同じ日にお金がなくなる
〔実際〕二人の初めの所持金５：３＝10：６ ⇒ミーちゃんが10日間よぶんに使える
ミーちゃんが10日間でよぶんに使う金額は600×10＝6000円で、これが10－９の１にあたります。
したがって、初めの所持金は、ミーちゃん＝6000×10＝60000円、ケイちゃん＝6000×６＝36000円とわかります。
※前半で「加比の理」と呼ばれる算数独特の考え方を使いました。こうした考え方になじんでいただかないと、算数の上達はなかなか望めません。この問題は、たまたまオトナが好きな（笑）方程式でも解けますが、そうは問屋が卸さない問題も算数にはたくさんあるのです。
|
Ｂ１０ 条件整理
３、６、９、12、15と書かれた５枚のカードがあります。これらのカードをＡ、Ｂ、Ｃ、Ｄ、Ｅの５人が１枚ずつ取ったとき、次のことがわかりました。
「ＢはＣの２倍より大きい」 「ＥはＤの２倍である」 「ＡとＤの和はＢと等しい」
Ａが取ったカードはいくつですか？
解答 ９
解説 ２つめの条件「Ｅ＝Ｄ×２」を満たすのは ①Ｄ＝３、Ｅ＝６ ②Ｄ＝６、Ｅ＝12 のいずれかです。それぞれを検討してみます。
①の場合 ３つめの条件が「Ａ＋３＝Ｂ」となり、これを満たすＡ、Ｂと残りのＣは (1)Ａ＝９、Ｂ＝12、Ｃ＝15 (2)Ａ＝12、Ｂ＝15、Ｃ＝９ が考えられます。しかし(1)、(2)ともに１つめの条件「Ｂ＞Ｃ×２」を満たさず、正解になる組合せはありません。
②の場合 ３つめの条件が「Ａ＋６＝Ｂ」となり、これを満たすＡ、Ｂと残りのＣは (1)Ａ＝３、Ｂ＝９、Ｃ＝15 (2)Ａ＝９、Ｂ＝15、Ｃ＝３ が考えられます。このうち(2)が１つめの条件「Ｂ＞Ｃ×２」を満たしています。
問題の条件をすべて満たす組合せは（Ａ＝９、Ｂ＝15、Ｃ＝３、Ｄ＝６、Ｅ＝12）となり、正解は９です。
|
Ｂ０９ 規則性
魔法の貯金箱があります。この貯金箱を１回たたくと、中に入っている金額が偶数ならば半額になり、奇数ならば３倍に１円を加えた金額になります。この貯金箱に52円入れ、箱を2011回たたくといくらになりますか？
解答 ２円
解説 ある程度の試行が必要です（○数字はたたいた回数）。①26円②13円③40円④20円⑤10円⑥５円⑦16円⑧８円⑨４円⑩２円⑪１円⑫４円⑬２円⑭１円…… このように⑨以降で４円、２円、１円が繰り返されることになります。３種類の繰り返しは、番号を３で割ったときの余りを手がかりにすることができ、2011÷３＝670余り１より、2011回たたいたときの金額は⑩や⑬などと同じ２円が正解となります。（10÷３＝３余り１、13÷３＝４余り１）
|
Ｂ０８ ニュートン算
一定の割合で水が流入して、あふれているタンクがあります。このタンクからポンプで水をくみ出します。ポンプ４台だと18分、ポンプ５台だと12分でタンクは空（カラ）になります。では、ポンプ10台だと何分で空になるでしょうか？？
解答 ９分
解説 与えられた２つの条件から、次の①、②を考えます。
①４台のポンプが18分でくみ出す水量は（タンクの満水量）＋（18分で流入する水量）です。１台のポンプが１分でくみ出す水量を１台×１分＝１とすると、この水量は４台×18分＝72と考えられます。
②５台のポンプが12分でくみ出す水量は（タンクの満水量）＋（12分で流入する水量）です。１台のポンプが１分でくみ出す水量を１台×１分＝１とすると、この水量は５台×12分＝60と考えられます。
①、②の差を考えると、太字部分では（６分で流入する水量）、赤い数字では72－60＝12です。これらが等しいことから（１分で流入する水量）＝12÷６分＝２とわかり、これを利用して（タンクの満水量）＝72－２×18分＝36が求められます。※60－２×12分＝36でも同じ
10台のポンプを使うと、１分で10台×１分＝10の水をくみ出すことができますが、（１分で流入する水量）が２あるから、実際に減っていく水量は１分で10－２＝８です。（タンクの満水量）＝72だから、タンクは72÷８＝９分で空になります。
※え？塾では線分図？ 確かにニュートン算は線分図を使って説明する先生が多いでしょう。しかし実際の入試で受験生がニュートン算を解くことを想定すると、この程度の基本ニュートン算は線分図ナシで済ませてほしいところです。試験は時間との戦いでもあります。線分図も決して悪くないですが、ニュートン算を線分図ナシという壁を越えてみてくださいね。
|
Ｂ０７ 倍数算
チョコレート5個とキャンディー12個が同じ値段です。チョコレートとキャンディーを１個につき5円ずつ値引きしたら、チョコレート４個とキャンディー11個が同じ値段になりました。値引き前の値段でチョコレートとキャンディーを10個ずつ買うと代金はいくらになりますか？
解答 850円
解説 値引き前はチョコレート５個とキャンディー12個が同じ値段だから、単価（１個の値段）の比はチョ：キャ＝12：５です。値引き後はチョコレート４個とキャンディー11個の値段が同じだから、単価の比はチョ：キャ＝11：４です。チョコレートもキャンディーも５円ずつ値引きしたから、単価の差は変わっていないはずです。
２つの比で単価の差に注目すると、値引き前、値引き後ともに７になっています（12－５も11－４も７）。このことは２つの比が同じ基準の比であることを示していて、値引き前後の単価の差にあたる１を５円と考えることができます（チョコなら12－11＝１。キャンディーの５－４＝１でも同じこと）。したがって値引き前のチョコ＝５円×12＝60円、キャンディー＝５円×５＝25円とわかり、これらを10個ずつ買ったときの値段は（60＋25）×10＝850円です。
※実際の算数の授業っぽく解説しました。これこそ子どもたちに届ける算数流です（笑）。算数に慣れていない人は解読に苦労しましたか？ さらに追いうちをかけるようですが、この問題は数値に恵まれ、２つの比の差が初めから７にそろっていましたが、そろっていないときは最小公倍数に一致させ、その後実際の金額と結びつけることになります。（ますます算数流深まる???）
|
Ｂ０６ 整数問題（２けたの４の倍数）
４枚のカードがあり、片面には１～４の数字がそれぞれ書かれています。また、もう片面には反対の面の数字と加えると９になる数字がそれぞれ書かれています。この４枚のカードを袋に入れ、２枚を引いて２けたの整数として並べるとき、４の倍数は何通り考えられますか？
解答 12通り
解説 ４枚のカードは次のようになっています。
片面 １ ２ ３ ４
反対 ８ ７ ６ ５
同じカードの両面を並べることはできないから、その点に注意して４の倍数を選んでいきます。モレが起きないように小さい順に考えます。12、16、24、28、32、48、52、56、64、68、76、84 以上12通りが考えられます。
※36や72を入れてしまった人、いますか？ 注意深くネ！
|
Ｂ０５ 差集め算（枚数の取り違え）
50円切手と80円切手を何枚かずつ買って1880円になる予定でしたが、枚数を逆に買ってしまったため、120円安くなりました。50円切手と80円切手をそれぞれを何枚ずつ買う予定でしたか？
解答 50円切手12枚 80円切手16枚
解説 まず、合計の値段が安くなっていることから、80円切手を多く買う予定が、枚数を逆にしたことで、50円切手を多く買ってしまった点を抑えてください。下のような図を書いてみると、左側の黒い数字の部分では代金に差が生じないから、120円の差は右側の赤い数字の部分で生じたことがわかります。つまり１枚について30円の差が４枚分集まって120円の差が生じたのです（120÷30＝４）。予定代金の1880円から80円切手が４枚多い分を差し引くと1560円（1880－80×４） これは図の黒い数字の部分の代金だから、1560÷（80＋50）＝12枚→黒い数字の部分の枚数（50円切手の予定枚数） 80円切手の予定枚数は４枚を加えて16枚です。
予定
80 80 …… 80 80 …… 80
50 50 …… 50
実際
80 80 …… 80
50 50 …… 50 50 …… 50
※トップページの「ご来場感謝のプレゼント」にも書きましたが、個数取り違えの問題では（合計代金の差）÷（単価の差）＝（買う個数の差）という考え方が知られています。
|
Ｂ０４ 周期算・日暦算
小野さんは３日に１回、小野さんの奥さんは４日に１回、整骨院のマッサージに通っています。５月８日の日曜日に二人がいっしょだったとすると、次に二人がいっしょになる日曜日は何月何日ですか？ 整骨院に休みの日はありません。
解答 ７月31日
解説 ご夫婦が一緒になるだけなら、３と４の最小公倍数で12日に１回です。これがさらに日曜日と一致するのは、一週間が７日であることから、12と７の最小公倍数で84日に１回となります。※３、４、７の最小公倍数は84
求める日付は５月８日の84日後。ひとまず５月の日付として考えると５月92日です（８＋84＝92）。これは５月の月末が31日であることから６月61日（92－31＝61）、さらに６月の月末が30日であることから７月31日（61－30＝31）にあたります。ひとまず開始月の日付で考え、正しい日付になるまで修正していく。子どもたちに人気のある考え方です。
|
Ｂ０３ 整数問題（現れる数字の和）
1から100までの整数を小さい順に並べ、次のような整数Aを作ります。
Ａ＝123456789101112………9899100
整数Ａの各位の数字の和を求めてください。
解答 901
解説 美しい解法を紹介しましょう。
１ケタの整数部分の十の位に０を補い、01、02、03、…、09と考えます。
さらに先頭に00を加えると 00、01、02、03、…、97、98、99のように２ケタの整数が100個並びます。
この100個の整数には合計200個の数字があり（それぞれが２ケタだから）、０～９までの10個の数字を公平に20個ずつ含んでいます。（何かが多くて何かが少ないということはない）
このことから00～99までの各位の数字の和は（０＋１＋２＋３+…+９）×20＝45×20＝900
ここに最後の100が百の位に持っている１を加え、正解は901となります。
|
Ｂ０２ 還元算
バスが何人かの客を乗せて出発しました。最初のバス停で客の1/3が降り、降りた客の1/4にあたる人が乗りました。２番目のバス停で12人が降り、乗った人はいませんでした。３番目のバス停で客の3/4が降り、４人が乗って客が10人になりました。出発したときの客は何人でしたか？、
解答 48人
解説 後ろの条件から戻っていきます。元に還（かえ）すという意味で還元算と呼ばれています。
最後の10人から、その前に乗った４人を引くと６人。
3/4が降りて６人になったから、６人が1/4にあたり、６÷1/4＝24人→３番目のバス停まで
これに降りた12人を加えて36人。→２番目のバス停まで
最初のバス停では1/3が降り、1/3×1/4＝1/12が乗ったから、1/3－1/12＝1/4の客が減ったことになり、バスに残った客は3/4。これが36人にあたるから、36÷3/4＝48人。これが出発したときの客の人数です。
|
Ｂ０１ いもづる算
５円玉、10円玉、50円玉の３種類の硬貨がたくさんあります。これらの硬貨を使って、合計の金額を155円にする方法は全部で何通りありますか？ ただし、どの硬貨も最低１枚は使うことにします。
解答 15通り
解説 「どの硬貨も最低１枚は使う」から、初めに全体の金額から、各硬貨を１枚ずつ差し引きます。
５＋10＋50＝65円、155－65＝90円。
次に、この90円を３種類の硬貨で作ることを考えます。
５円玉を○枚、10円玉を□枚、50円玉を△枚とすると、５×○＋10×□＋50×△＝90。
この式は５、10、50の最大公約数５で割っても影響がなく、１×○＋２×□＋10×△＝18。
初めに１枚ずつ差し引いているから○、□、△にあてはまるのは０を含む整数です。
こうした式は係数（かけられている数）が大きい△を主役に、二番目に係数が大きい□を準主役にして検討するのがコツです。下のような要領です。
△＝０のとき、□にあてはまる整数は０～９までの10通り。
△＝１のとき、□にあてはまる整数は０～４までの５通り。
△に２以上の整数は入れられないから、10＋５＝15通りが解答となります。
※初めに１枚ずつ差し引く作業をせずに式を作っても解けますが、式の数値はなるべく小さくした方がよいでしょう。
|
東京近郊で中学受験を目指すお子様への算数家庭教師はさんじゅつまんにお任せください。
下記リンク「中学受験算数家庭教師について」をお読みになり、そのページ内に設置してあるフォームよりご連絡ください。
|
どうでしたか？ できましたか？