 �a�S�P�@ �a�S�P�@ �����Z �����Z
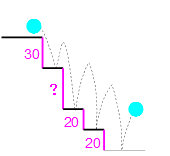
����{�[�������i�䂩�j�ɗ������Ƃ��A���Ƃ���������60�������͂ˏオ��܂��B���}�̂悤�Ȓi�ŏォ�痎�Ƃ����Ƃ���A��ԉ��̏���30cm�͂ˏオ��܂����B�ォ��Q�i�ڂ̍����H�͉�cm�ł����H�@���}���̐��l�͊e�i�̍����������A�P�ʂ�cm�ł��B
�@32����
����@�S��̃o�E���h���@�A�A�A�B�A�C�Ƃ��܂��B
�@�@30��������������30�~0.6��18�����͂ˏオ��܂��B
�C�@�͂ˏオ�肪30����������A30��0.6��50���������܂����B
�B�@�͂ˏオ�肪50�|20��30����������50���������܂����B
�A�@�B�Ɠ����ł��B
�H���A�̗������������@�̂͂ˏオ��̍�������A50�|18��32�����ł��B
|
 �a�S�O�@ �a�S�O�@ �K���� �K����
����������K���ɂ��������Ď��̂悤�ɕ���ł��܂��B
�P�A�P�A�Q�A�P�A�Q�A�R�A�P�A�Q�A�R�A�S�A�P�A�Q�A�R�A�S�A�T�A�c�c
10��10���܂łɁA�`�͂R�~�`��܂��B�`�͂����ł����H
�@�T
����@�@(�P)�A(�P�A�Q)�B(�P�A�Q�A�R)�C(�P�A�Q�A�R�A�S)�D(�P�A�Q�A�R�A�S�A�T)�c�c�̂悤���ԍ������đg�������Ă݂�ƁA�e�g�Łq�P�r����q�ԍ��Ɠ������r�܂Ő�������ł��邱�Ƃ��킩��܂��B10�����߂Č����̂��I�g�ŁA10��10��ڂɌ����̂��R�g��10�Ԗڂł��B�R�g��10�Ԗڂ܂łɂ��ꂼ��̐����������l����Ǝ��̂悤�ɂȂ�܂��B
�P��19��@�Q��18��@�R��17��@�S��16��@�T��15��@�U��14��@�V��13��@�W��12��@�X��11��@10��10��
11���W��@12���V��@13���U��@14���T��@15���S��@16���R��@17���Q��@18���P��
���̂Ȃ��Ō��������̐����g�̂R�{�ɂȂ��Ă��鐔�͂T�ł��B
������Ȃ̂ł��ׂĂ̐��̉������܂������A���̐��Ɖ̔{���͏������Ȃ���������A���ۂɂ͂T�~�R��15�킩�������_�Ō�������Ă悢�Ǝv���܂��B
|
 �a�R�X�@ �a�R�X�@ �ꍇ�̐� �ꍇ�̐�
�P�P�^�̐����P�A�Q�A�R�A�c�c�A�X�������ꂽ�J�[�h���P��������܂��B�i�P�`�X�e�P���A���v�łX���j
�ׂ荇�����������g�킸�ɂQ�P�^�̐��������Ƃ��A�S���ʼn��ʂ�̐������ł��܂����H
�@56�ʂ�
����@�\�̈ʂ��P���X�i�Q�ʂ�j�ɂ���ƈ�̈ʂ͂V�ʂ肸����܂��B���Q�~�V��14�ʂ�c�A�@�܂��A�\�̈ʂ��Q�`�W�i�V�ʂ�j�ɂ���ƈ�̈ʂ͂U�ʂ肸����܂��B���V�~�U��42�ʂ�c�C�@�@�A�ƃC�����v���ĉ�56�ʂ�ł��B
��10����99�܂łQ�P�^�̐�����90����܂��B��������10��20�̂悤�Ɉ�̈ʂ��O�̂��́i�X�j12�A21�A23�̂悤�ɗׂ荇�����������Ԃ��́i16�j11�A22�A33�̂悤�ȃ]���ځi�X�j�������Ă��悢�Ǝv���܂��B
|
 �a�R�W�@ �a�R�W�@ ����Z�Ɨ]�� ����Z�Ɨ]��
����W��̎Q���҂�200�l�ȏ�300�l�ȉ��ł����B�Q���҂��O���[�v��������Ƃ��A24�l���̃O���[�v������Ă����ƂP�̃O���[�v������21�l�ɂȂ�܂����B�܂��A30�l���̃O���[�v������Ă����ƂR�̃O���[�v��27�l���ɂȂ�܂����B�W��̎Q���҂͑S���ʼn��l�ł����H
�@261�l
����@24�l���̃O���[�v������21�l���܂邩��A�Q���҂̐l����24�̔{�����21�傫���l���ł��B�c�A
�܂��A30�l���̃O���[�v������27�~�R��81�l��30�l�O���[�v����͂���Ă��āA����81�l��30�l�O���[�v�ɒ�����81��30���Q���܂�21���A30�l���̃O���[�v��������Ƃ���21�l���܂邱�Ƃ��킩��܂��B���������ĎQ���҂̐l����30�̔{�����21�傫���l���ł��B�c�C
�A�A�C���Q���҂̐l����24��30�̌��{�����21�傫���l���Ƃ킩��A24��30�̍ŏ����{����120������A�Q���҂̐l����120�~���{21�l�ƕ\�����Ƃ��ł��܂��B�q�Q���҂̐l��200�l�ȏ�300�l�ȉ��r�̏�������A���ɂQ�����Ă͂߂�261�l�������ƂȂ�܂��B
����13�u���̉ߕs���Z�ƕ��͋C�����Ă��܂����A����̓O���[�v�̐��ɏ������Ȃ����߉ߕs���Z�Ƃ͂������܂��B��T�u���Ő�����������Z�̂��܂�Ɋւ�����ł��B
|
 �a�R�V�@ �a�R�V�@ ���� ����
���[�O���g�P���ɋ����T����������ƁA���̓��ɂ͐V�������[�O���g���U���ł��܂��B�_���r�N�̉Ƃł͖����������č�������[�O���g�̂Q�^�R��H�ׁA�c��̃��[�O���g�ɂ��̂T�{�̋����������ĐV�������[�O���g������Ă��܂��B
�����10���̃��[�O���g�ɋ����������ă��[�O���g�����n�߂܂����B���n�߂Ă���T����ɂ́A��������ł����̂ŐH�ׂ�O�ɋߏ��̉Ƃɕ����Ă����܂����B�����Ďc��̃��[�O���g�̂Q�^�R��H�ׂĂ���A���܂łƓ����悤�Ƀ��[�O���g���������A���̂Q����ɂł������[�O���g��1440���ł����B�ߏ��̉Ƃɂ��������[�O���g�͉����ł������H
�@600��
����@
| |
|
�P���� |
�Q���� |
�R���� |
�S���� |
�T���� |
�P���� |
�Q���� |
| �ł���� |
--- |
60���U |
120�� |
240�� |
480�� |
960����360�� |
720�� |
1440�� |
| �H�ׂ����Ƃ̗� |
10���P |
20���Q |
40�� |
80�� |
160�� |
120�� |
240�� |
--- |
���߂̃��[�O���g���P�Ƃ���ƁA�����������邱�Ƃŗ����U�{�̃��[�O���g�ɑ����A
���̌�2/3��H�ׂ���U�~(�P�|2/3)���Q���c��܂��B���̂悤�ɂU�{�A1/3�{�𑱂���ƁA�ł���ʂ��H�ׂ����Ƃ̗ʂ��O�̓��̂Q�{���������ƂɂȂ�܂��B
�T����ɂł���ʂ�960���ł����A�ŏI�I�ȃ��[�O���g��1440��������A�O�̓��ɂł���ʂ�1440���Q��720���A���̑O�̓��ɂł���ʂ�720���Q��360���̂͂��ł��B���������ĂT����ɋߏ��ɂ���������960�|360��600���ł��B
|
 �a�R�U�@ �a�R�U�@ ����Z�i�����̗j���̉j ����Z�i�����̗j���̉j
 ����N�̂R���͌��j���Ɩؗj�����S�ł����B ����N�̂R���͌��j���Ɩؗj�����S�ł����B
�@���̔N�̂R���R���͉��j���ł����H
�@���j��
����@�R���͑�̌��Ō�����31���ł��B31�����V���S�T�Ԃ��܂�R��������A��̌��ɂ͂S�T�ő��肸�ɂT�T�ɂȂ�j�����R����܂��B���j���Ɩؗj�����S��Ȃ�A���̊Ԃɂ���Ηj���Ɛ��j�����S��̂͂��ŁA�T��ɂȂ�j���͋��j�A�y�j�A���j�ł��B���̔N�̂R���͋��j�n�܂�̖ؗj�I���ŁA�R���R���͓��j���ł��B
�j���@���y�����ΐ���
�@�T�T�T�S�S�S�S
|
 �a�R�T�@ �a�R�T�@ �������i�Q���̐����̘a�j �������i�Q���̐����̘a�j
�S�̐����`�A�a�A�b�A�c������A���̏��ɑ傫���Ƃ��܂��B�i�`���a���b���c�j
���̂S�̐����̂����A�Q�̐��������o���Ă��̘a�����߂�ƁA���̂T�ʂ�ɂȂ�܂����B
134�C121�C109�C97�C84
�S�̐����`�A�a�A�b�A�c�͂��ꂼ�ꂢ���ł����H
�@�`73 �a61 �b48 �c36
����@�S�̐�������Q�̐��������o���ƁA���\�A�`�J�̂悤�ɑS���łU�ʂ�̎��o����������܂��B
| |
�` |
B |
C |
D |
�a |
| �A |
�� |
�� |
|
|
134 |
| �C |
�� |
|
�� |
|
121 |
| �E |
�� |
|
|
�� |
109 |
| �G |
|
�� |
�� |
|
109 |
| �I |
|
�� |
|
�� |
97 |
| �J |
|
|
�� |
�� |
84 |
�`���a���b���c�̏�������A�����Ƃ��a���傫���Ȃ�̂̓A)�`�{�a�A�����C)�`�{�b�A�t�ɂ����Ƃ��a���������Ȃ�̂̓J)�b+�c�A���ɏ������Ȃ�̂��I)�a�{�c�ł��B
���ł͂T�ʂ�̘a�����^�����Ă��܂��A����͘a�������ɂȂ�g���������邱�Ƃ������Ă��āA�E)�`�{�c�ƃG)�a�{�b�͓����l�ł��B
������ȊO�͑召�̏����͂����肷�邩�瓯���l�ɂ͂Ȃ肦�܂���B
�U��ނ̘a�����ׂĉ�����ƁA�`�`�c�����ꂼ��R���v�����l�ɂȂ�܂��B�i���̐����R�R���j
134�{121�{109�{109�{97�{84��654���`�`�c�R�̘a
654���R��218���`�`�c�̘a
���Ƃ̓E�I����`�a�̍���12�A�A�C����a�b�̍���13�A�C�E����b�c�̍���12�Ƃ킩�邩��A�a���Z���g���āi�����}�������Ă��������j�S�̐��������ׂċ��߂邱�Ƃ��ł��܂��B
|
 �a�R�S�@ �a�R�S�@ �����Z �����Z
�h���~����́A���j����70�~�A���j����60�~�A�Ηj����50�~�A���j����40�~�A�ؗj����30�~�A���j����20�~�A�y�j����10�~���������邱�Ƃɂ��܂����B���j������n�߂āA�h���~����̒a�����ɒ����z�ׂ���10540�~�ł����B�h���~����̒a�����͉��j���ł����H
�@�Ηj��
����@��T�Ԃ̒����z��70�{60�{50�{40�{30�{20�{10��280�~�ł��B10540��280��37���܂�180������A���j���ɒ������n�߂Ă���37�T�Ԍo�ߌ��180�~�s�����܂��B���̏T�̏��߂̂R���Ԃ�70�{60�{50��180�~�ɂȂ邩��A�h���~����̒a�����͓��j������R���ڂ̉Ηj���ł��B
|
 �a�R�R�@ �a�R�R�@ �v�Z�i�u���b�N�{�b�N�X�j �v�Z�i�u���b�N�{�b�N�X�j
����u���b�N�{�b�N�X�i����̌v�Z������@�B�j�ɐ�������͂���ƁA
���̇@�`�C�̌v�Z��A�����čs���A�v�Z���ʂ��o�͂��܂��B
�@�@�T��������
�@�A10�Ŋ���
�@�B������P�ʂ��̂Ă�
�@�C10�{����
�v�Z���ʂƂ���50���o�͂���܂����B���͂��������͂����ł����H�l�����鐮�������ׂē����Ă��������B
�@45 46 47 48 49 50 51 52 53 54
����@�v�Z�C�̎�O��50��10���T�A�B�̎�O�łT�ȏ�U�����A�q10�{���ār�A�̎�O��50�ȏ�60�����A�q�T�������ār�@�̎�O��45�ȏ�55�����ł��B���͂������͐���������A45�ȏ�55�����̐����������ƂȂ�܂��B
|
 �a�R�Q�@ �a�R�Q�@ ���邤�N ���邤�N
���邤�N�̂��܂�͎��̂悤�ɂȂ��Ă��܂��B
�@�u����̔N�����S�̔{���̔N�����邤�N�Ƃ���v
�@��O�@�u�S�̔{���ł����Ă�100�̔{���̔N�͂��邤�N�Ƃ��Ȃ��v
�@��O�A�u100�̔{���ł����Ă�400�̔{���̔N�͂��邤�N�Ƃ���v
�ł́A���N�̐���2012�N���琼��3000�N�܂łɁA���邤�N�͉���܂����H
�@240��
����@2012����3000�܂ł̂S�̔{���́A�i3000�|2012�j���S+�P��248�ł��B���{�P�ɒ��ӁI�i�A�؎Z�j
���̂����A��O�@�ɊY������100�̔{����2100�A2200�A�c�c�A2900�A3000��10����A��O�A�ɊY������400�̔{�����Q����܂��i2400��2800�j�B���������Ă��邤�N�̉͑S����248�|10�{�Q��240��ł��B
|
 �a�R�P�@ �a�R�P�@ ���l�Z�i�R�l�j ���l�Z�i�R�l�j
�`����͕���120���A�a����͕���60���A�b����͕���30���̑����ŕ����܂��B3600�����ꂽ�o�A�p�Q�n�_������A�`����Ƃb����͂o�n����p�n�Ɍ������A�a����͂p�n����o�n�Ɍ������R�l�������ɏo�����܂��B�`����͂a����Əo������Ƃ��A������ς��Ăo�n�̕��ւ��ǂ�A�b����Əo������Ƃ��A�Ăь�����ς��Ăp�n�Ɍ������܂��B�`����Ƃa���Q�x�ڂɏo��n�_�͂o�n���牽�����ꂽ�Ƃ���ł����H
�@1440��
����@
���}�̍������o�n�A�E�����p�n
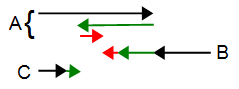 �t������߂Â��Ƃ��A�o��܂łɂ����鎞�Ԃ́q����Ă��鋗���r���q�����̘a�r�ŋ��߂܂��B�܂��A���������ɐi�ނƂ��A����鋗���́q�����̍��r�~�q���ԁr�ł��B �t������߂Â��Ƃ��A�o��܂łɂ����鎞�Ԃ́q����Ă��鋗���r���q�����̘a�r�ŋ��߂܂��B�܂��A���������ɐi�ނƂ��A����鋗���́q�����̍��r�~�q���ԁr�ł��B
�����������i�K�ł��B�`�Ƃa��3600���i120�{60�j��20���ŏo��܂��B���̂Ƃ��`�Ƃb�́i120�|30�j�~20��1800������Ă��܂��B
�̐������i�K�ł��B�`�Ƃb��1800���i120�{30�j��12���ŏo��܂��B���̂Ƃ��`�Ƃa�́i120�|60�j�~12��720������Ă��܂��B�Ԃ�������O�i�K�ł��B�`�Ƃa��720���i120+60�j���S���ŏo��܂��B
�R�̒i�K�����v����Ƃa�̕��������Ԃ�20�{12�{�S��36���ŁA�a�̕�����������36�~60��2160���ł��B�a�͂p�n��������n�߂�����A�o�n����̋�����3600�|2160��1440���ł��B
|
 �a�R�O�@ �a�R�O�@ �v�Z�̍H�v�i���̘a�j �v�Z�̍H�v�i���̘a�j
���i�N�N�j�̈�̒i�����̒i�܂łɂ�9�~9��81��ނ̌v�Z������܂��B�u�C���C�`���C�`�v����u�N�N�n�`�W���E�C�`�v�܂łł��B����81��ނ̌v�Z���ʂ����ׂĉ������a�����߂Ă��������B
�@2025
����@��̒i�̐ς̍��v�͂P�~�P+�P�~�Q+�c+�P�~�X���P�~�i�P+�Q+�c+�X�j�A��̒i�̐ς̍��v�͂Q�~�P+�Q�~�Q+�c+�Q�~�X���Q�~�i�P+�Q+�c+�X�j�̂悤�ɕ\�����Ƃ��ł��܂��B�����悤���O�̒i������̒i�܂����~�i�P+�Q+�c+�X�j�ƕ\�����Ƃ��ł��邩��A���̂��ׂĂ̐ς̍��v�́i�P+�Q+�c+�X�j�~�i�P+�Q+�c+�X�j��45�~45��2025�ł��B
|
 �a�Q�X�@ �a�Q�X�@ �L���i�̘a�j �L���i�̘a�j
�����`�̖̘a���m�`�n�ŕ\���܂��B���Ƃ��� �m�U�n���P�{�Q�{�R�{�U��12�ł��B
�m18�n�|�m�a�n���m31�n�ƂȂ�悤�Ȑ����a�����߂Ă��������B
�@�S
����@�k18�l���P+�Q�{�R�{�U�{�X�{18��39�@�k31�l���P�{31��32������A�k�a�l��39�|32���V�ł��B�̘a���V�ɂȂ邱�Ƃ���a���U�ȉ��̐����ł��邱�Ƃ͖��炩�ł��i�ǂ�Ȑ����ł��K���P�Ƃ��̐����g���ɂȂ邩��j�B�U�ȉ��̐����Ŗ̘a���V�ɂȂ鐮����T���ƂS�������Y�����邱�Ƃ��킩��܂��B�i�k�S�l���P�{�Q�{�S���V�j�@�����͂a���S�ł��B
|
 �a�Q�W�@ �a�Q�W�@ �ꍇ�̐��i�F�̓h��킯�j �ꍇ�̐��i�F�̓h��킯�j
�܂������ɕ��ԂS���̌��Ĕ���Z������ݒ��ł��B�����̐F���A�ƂȂ荇���Z������F�ɂȂ�Ȃ��悤�ɁA�s���N�A�N���[���A�u���[�̂R�F���ׂĂ��g���ēh�i�ʁj�肽���Ǝv���܂��B�h����͑S���ʼn��ʂ肠��܂����H
�@18�ʂ�
����@�S���̏Z����A�A�C�A�E�A�G�@�R�F���o�A�b�A�a�Ƃ��܂��B
�܂����߂Ɂu�ƂȂ荇���Z������F�ɂȂ�Ȃ��悤�Ɂv�p�^�[���̐����l���܂��B�A�̐F�͂R�ʂ�A�C�̐F�̓A�̐F�������Q�ʂ�A�E�̐F�̓C�̐F�������Q�ʂ�A�G�̐F�̓E�̐F�������Q�ʂ�ƂȂ�A���̍��v�͂R�~�Q�~�Q�~�Q��24�ʂ�ł��B
�������I
����24�ʂ�́u���ׂĂ̐F���g���v�Ƃ����������l���Ă��܂���B�܂�A�o�b�o�b�̂悤�ȃP�[�X���܂܂�Ă���̂ł��B���̂悤�ȂQ�F���������Ⴂ�ɂȂ�p�^�[���͂o�b�o�b�A�b�o�b�o�A�o�a�o�a�A�a�o�a�o�A�b�a�b�a�A�a�b�a�b�̂U�ʂ�ł��B
24�ʂ肩�炱�̕������������A��18�ʂ�ł��B
|
 �a�Q�V�@ �a�Q�V�@ �s�v�c�ȏ��� �s�v�c�ȏ���
��i���j�̍���70�Ɣ���30������܂��B����������ĂQ�̔��ɕ�������A�P�̔��̍��̐����A�����P�̔��̔��̐����12�����Ȃ��Ă��܂����B�Q�̔��̂��������Ă����̐����������́A���Ɣ������킹�ĉ������Ă��܂����H
�@58��
����@�\��p�ӂ��܂����B���`�̔������A���a�̍������{12�Ƃ��āA�A�C�E�̏��ɍl���܂��B
| |
�� |
�� |
�v |
| ���` |
�A |
�� |
�C |
| ���a |
��+12 |
�G |
�E |
| �v |
70 |
30 |
100 |
�A�c70���灠��12����������������A58��聠���Ȃ����ł��B
�@�@�A��58�|����
�C�c58�|���Ɓ��̍��v������58�ł��B�C��58��
�E�c�S����100������A100����C�������ƃE�����߂��܂��B�E��42��
���v�̂��������͔̂��a�ŁA������58�ł��B
���������s�����Ă��邽�߁A���������ł��邩�����߂邱�Ƃ͂ł��܂���B�������A�����g�����������ɑ��삷�邱�ƂŁA���ꂼ��̔��̍��v�̌���m�邱�Ƃ��ł��܂��B������ƕs�v�c�Ȗ��ł����ˁB
���G�E�C�̏��ɍl���Ă������Ƃ��ł������ł��B
|
 �a�Q�U�@ �a�Q�U�@ �T�C�R���̍\�� �T�C�R���̍\��
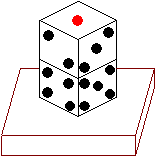 ���Ɏ������悤�ɁA��̏�ɂQ�̃T�C�R�������Ăɏd�Ȃ�悤�ɒu���܂��B���̂Ƃ��A�����Ă���ڂ̐���S���������ς��l���܂��B���̗�̏ꍇ�͂P�~�Q�~�R�~�T�~�S�~�S�~�T�~�R�~�Q��14400�ƂȂ�܂��B���낢��ȃT�C�R���̒u�����̂Ȃ��ŁA�����Ă���ڂ̐���S���������ς��ő�ɂȂ�Ƃ��A���̍ő�̐ς͂����ł����H ���Ɏ������悤�ɁA��̏�ɂQ�̃T�C�R�������Ăɏd�Ȃ�悤�ɒu���܂��B���̂Ƃ��A�����Ă���ڂ̐���S���������ς��l���܂��B���̗�̏ꍇ�͂P�~�Q�~�R�~�T�~�S�~�S�~�T�~�R�~�Q��14400�ƂȂ�܂��B���낢��ȃT�C�R���̒u�����̂Ȃ��ŁA�����Ă���ڂ̐���S���������ς��ő�ɂȂ�Ƃ��A���̍ő�̐ς͂����ł����H
�@86400
����@��̃T�C�R���͌����Ȃ��ʂ��P�ʂ�����A�P�̖ʂ��B���ƌ�����ʂ̐��̐ς��ő�ɂȂ�܂��B�܂��A���̃T�C�R���͌����Ȃ��ʂ��Q�ʂ�����A���s���P���U�̖ʂ��B���ƌ�����ʂ̐��̐ς��ő�ɂȂ�܂��B���������Đ����́i�Q�~�R�~�S�~�T�~�U�j�~�i�Q�~�R�~�S�~�T�j��86400�ł��B
���T�C�R���̕��s�Ȗʂ̘a�͂V�ł��B�P���U�̖ʂ�������悤�ɂ����Ƃ��ς͂P�~�U���U�{�ł����A�Q���T�̖ʂł͂Q�~�T��10�{�A�R���S�̖ʂł͂R�~�S��12�{������A�ςւ̉e�����P���U���B�����Ƃ�����ԑ傫���Ȃ�܂��B
|
 �a�Q�T�@ �a�Q�T�@ �{���Ƃ��܂� �{���Ƃ��܂�
�X���������12�̔{���ɂȂ�A12��������ƂX�̔{���ɂȂ鐮��������܂��B���̂悤�Ȑ�����200�ɂ����Ƃ��߂����������߂Ă��������B
�@195
����@�����ɂ��Ă͂܂鐮�������Ƃ���ƁA��+�X��12�̔{��������A�����12�����������{21��12�̔{���ł��B�܂��A��+12���X�̔{��������A����ɂX����������+21�͂X�̔{���ł��B�����̂��Ƃ��灠+21��12�̔{�����X�̔{���A�܂�12�ƂX�̌��{���Ƃ킩��܂��B
12�ƂX�̍ŏ����{����36������A���{����36�A72�A�c�c�A180�A216�A252�A�c�c
��������21���������l����������A�����Ƃ�200�ɋ߂����̂�216�|21��195�ƂȂ�܂��B
|
 �a�Q�S�@ �a�Q�S�@ �����Ɣ� �����Ɣ�
�X�q����Ɛ^������͓����h����Ɏn�߂܂����B�͂��߁A�X�q����Ɛ^������̏h������Ȃ��X�s�[�h��15�F14�ł������A�X�q����͔������I�����Ƃ���ŃX�s�[�h��0.8�{�ɂ��܂����B�^������̓X�s�[�h���Ō�܂ŕς�����1����30�����傤�ǂŏI���܂����B�X�q���h����I����̂ɂ͂ǂꂾ���̎��Ԃ�������܂������H
�@�P����34��30�b
����@��l�̏h��̗ʂ͓���������A�h������Ȃ��X�s�[�h�Əh����I���鎞�Ԃ͔����i�䂪�t�ɂȂ�j���܂��B
�h������Ȃ��X�s�[�h�@�F�^��15�F14�@���@�h����I���鎞�ԁ@�F�^��14�F15
�X�q����͔����̎����V�i14���Q�j���������Ƃ��A�X�s�[�h��0.8�{�i��4/5�{�j�ɗ��Ƃ�������A�c������Ȃ����Ԃ��V�~5/4���W��3/4�ɂȂ�A�ŏ����V�����킹��ƑS����15��3/4�̎��Ԃ�������܂��B
����^������̂����鎞�Ԃ�15������A���߂ē�l�̎��Ԃ𐮐���ŕ\���ƁA�F�^��15��3/4�F15��63�F60��21�F20�ł��B����20��90���i���P����30���j�ɂ����邩��A21�ɂ����鎞�Ԃ�90�~21/20��94.5���B�P�ʂ��ĂP����34��30�b�������ɂȂ�܂��B
|
 �a�Q�R�@ �a�Q�R�@ �̐� �̐�
�����̂�����܂��B���̒����̂̂��Ă̒������Q�������������100����3�A���̒������R�������������120����3�A�������S�������������80����3���ꂼ��̐ς������܂��B���Ƃ̒����̂̑̐ς͉�����3�ł����H
���@200����3
����@���Ă̒������������A���̒������������A�������������Ƃ��܂��B���Ă̒����������Q�������������Ƃ��A���̒����ƍ����͕ς��Ȃ�����A���~���~�Q��100�����~����50�c�A�@�Ƃ����������܂��B�����悤�Ɂ��~���~�R��120�����~����40�c�C�@���~���~�S��80�����~����20�c�E�@�ł��B
�A�ƃC�̎��������ăE�̎��Ŋ���Ɓi���~���j�~�i���~���j���i���~���j�����~���ƂȂ�A�����Q�����Ƃ��̒l�����߂��܂��B���~����50�~40��20��100���Q����100�ɂȂ遢��10�i�����j
���Ƃ́���10���A�̎��ɂ��Ă͂߂ā����T�i���j�A�C�̎��ɂ��Ă͂߂�Ɓ����S�i�^�e�j�ł��B���������Ē����̂̑̐ς͂S�~�T�~10��200����3�Ƌ��߂��܂��B
|
 �a�Q�Q�@ �a�Q�Q�@ �邩�ߎZ �邩�ߎZ
�o�Ɩ��ŃW�����P�������Ă���҂��邱�Ƃɂ��܂����B�u���ĂS�{�A������ƂQ�{���炦�邪�A�������̏ꍇ�͂��炦�Ȃ��v�Ƃ������[����16��W�����P�������܂����B���̌��ʁA�o��36�{�A����30�{�̂���҂���ɓ���܂����B�������̉Ǝo�����������A���ꂼ�ꋁ�߂Ă��������B
�@�������T���@�o�̏����V��
����@���������ƁA�P��ɂ��ĂS�{�Q���U�{�̂���҂��n����܂��B�o���̍��v��36�{30��66�{�̂���҂�������Ă��邩��A������������66���U��11��A�������̉�16�|11���T��Ƃ킩��܂��B
�����o��11���O�s�̂Ƃ��A�o�̂���҂͂S�~11��44�{�ɂȂ�܂����A���ۂɂ�36�{������W�{�i44�|36�j���Ȃ��Ȃ��Ă��܂��B�����������ɕς��Ƃ��炦��{�����S�|�Q���Q�{���邩��A�o���W���Q���S���Ă��邱�Ƃ��킩��܂��B�o����������11�|�S���V��ł��B
��㔼�͂邩�ߎZ�ł��B11/30wed�̖��ł͐��l���傫�������̂Ŗʐϐ}�������܂������A���̖��͐��l���������̂ŁA�ЂƂ܂��o��S���Ɖ��肵�A���ۂƂ̃Y�����畉���ׂ̉܂����B�ʐϐ}���������ɁA���������l�����Ȃ��ĉ��������A���邩�ߎZ�̖{���ɔ����Ă���Ƃ�������ł��傤�B
|
 �a�Q�P�@ �a�Q�P�@ �K���� �K����
�Q�̐����̑g�����̂悤�ȏ��Ԃŕ��ׂĂ����܂��B
�i�P�C�P�j�i�P�C�Q�j�i�Q�C�P�j�i�P�C�R�j�i�Q�C�Q�j�i�R�C�P�j�i�P�C�S�j�i�Q�C�R�j
�i�R�C�Q�j�i�S�C�P�j�E�E�E�E�E
���߂���150�Ԗڂ̑g���Ă��������B
�@�i14�C�S�j
����@�i�P�C�P�j|�i�P�C�Q�j�i�Q�C�P�j|�i�P�C�R�j�i�Q�C�Q�j�i�R�C�P�j|�i�P�C�S�j�i�Q�C�R�j�i�R�C�Q�j�i�S�C�P�j|�E�E�E�E�E
�b�ŋ�����悤�ɁA���E�̐��̘a��(1)�Q�̃O���[�v�A(2)�R�̃O���[�v�A(3)�S�̃O���[�v�A(4)�T�̃O���[�v�A�c�c�Ƒ����Ă��܂��B��( )���̓O���[�v�ԍ�
(1)�ɂ͂P�A(2)�ɂ͂Q�A(3)�ɂ͂R�A�c�̑g�����邩��A�������P���珇�ɉ������a��150�ɋ߂Â��Ƃ��ׂ�ƁA�P����16�܂ł̘a��136�ł��B��150���Ȃ��͈͂ōl���܂�
�܂�(16)�̃O���[�v���I������Ƃ����136�̑g������邱�ƂɂȂ�A150�Ԗڂ̑g�Ƃ�(17)�̃O���[�v��14�Ԗڂ̑g�ł��i150�|136��14�j�B(17)�̃O���[�v�͍��E�̐��̘a��18�ŁA���̐��͂P���珇�ɑ����Ă�������14�Ԗڂł�14�A�E�̐���18�|14���S�ł��B���������ĉ́i14�C�S�j�Ƌ��߂��܂��B
|

�����ߍx�Œ��w��ڎw�����q�l�ւ̎Z���ƒ닳�t�͂���܂�ɂ��C�����������B
���L�����N�u���w�Z���ƒ닳�t�ɂ��āv�����ǂ݂ɂȂ�A���̃y�[�W���ɐݒu���Ă���t�H�[����育�A�����������B
|

