今回は過不足算という文章題について解説します。目立たせようとして、また変わったタイトルをつけましたが、お読みになれば最後は納得してもらえると思います。


ではまず過不足算を１問紹介します。典型的な基本の過不足算です。

この過不足算の解き方は、算数でもいろいろあります。面積図や線分図なんかが主流かな。
ボクはどちらも使わない〈さんじゅつまん方式〉が好きです。あ、もちろん XとY の連立方程式は勘弁してくださいよ。それは算数の解法アクセスとしては、政府専用機（笑）くらい生徒たちの感覚からかけ離れてしまいます。
では〈面積図〉と〈さんじゅつまん方式〉を解説しましょうか。

面積図による解法



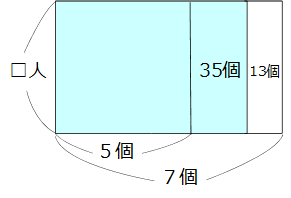
上のような面積図を書いて考えます。
タテが子どもの人数、横が分けるときの個数です。５個ずつ分けると35個あまり、７個ずつ分けると13個不足することが表現されています。カラーで表示した部分がキャンディーの総数ですね。

計算は簡単です。
子どもの人数＝（35＋13）÷（７－５）＝48÷２＝24人
キャンディーの総数は、カラー表示の部分の面積を求めて
24×５＋35 または 24×７－13
どちらで計算しても155個と求められます。

さんじゅつまん方式
同じパターンの面積図をいつも書くのは疲れるから、ボクは面積図を書かずに次のようなメモでもいいよと教えます。

　５ずつ　　35あまる

　７ずつ　　13不足

差をとる　　２　　　　48
割る　48÷２＝24人　これがの人数

あとはどちらかの条件に子どもの人数をあてはめて、
24×５＋35＝155個…キャンディーの総数
【重要な注意】
〈あまり〉と〈不足〉の差はたし算します。 〈あまり〉どうし、〈不足〉どうしは引き算でよいです。


さて次。
こんなに楽しくてわかりやすい過不足算ですが、少しストーリーが変化すると、
突然生徒たちの正解率が下がります。　こんな過不足算です。

これね。
これがタイトルに書いた「キャンディーが子どもで、子どもが旅館」の問題です。
じゃあ〈面積図〉はカットして、〈さんじゅつまん方式〉で解説します。

　７ずつ　　36あまる

　９ずつ　　22不足　←９人部屋の３つが５人、０人、０人だから(９－５)＋９×２＝22人不足

差をとる　　２　　　　58
割る　58÷２＝29部屋　これがの数

あとはどちらかの条件に部屋の数をあてはめて、
29×７＋36＝239人…合宿参加者の人数

どうでしたか～？
初めの問題は子どもたちにキャンディーが配られるという理解しやすいストーリーだったのですが、２問目の問題では旅館の部屋に子どもたちが配られているのですね。
まったく同じ仕組みの問題なのですが、とかく人間さまはワガママなもので、キャンディーのときにはちゃんと理解できたことが、人間さまがキャンディーの役割になった途端、プライドが許さないのかガタッと正解率が下がってしまうのです（本当）。

この講座を読んでくれたみなさんは、子どもがキャンディーをもらっても、旅館が子どもをもらっても、しっかり同じように解いてくださいね。

では今回の算数講座はこれで終わります。またどんどん講座を書きますから、これからも読みに来てくださいね！

カーテンコール
途中で、差をたし算で求める部分がありました。これは算数にマイナスの数がないことから起きる独特な説明方法です。２万円のもうけと３万円の損失の差が１万円ではなく５万円になるように、内容が逆のものごとの差はたし算です。あまりと不足は逆のことなので、たし算して差を求めます。