今回の第16講座は「同じ比どうしを合わせても同じ比」という加比の理（かひのり）と呼ばれる考え方を図形の問題に応用するお話です。理解してもらえたら図形のレベルアップは間違いないでしょう。


ではまず簡単な例で加比の理について説明しておきます。

優子さんが2000円、さおりさんが1500円持っていたとしましょう。
２人の所持金の比は？　そう、４：３です。
この２人が親切なマナベさんからおこづかいをもらいました。
年上の優子さんが400円、さおりさんが300円です。
もらったおこづかいの比は？　えぇ、これも４：３です。

では、初めの所持金に、もらったおこづかいを加えてみましょう。
優子さんは 2000＋400＝2400円、さおりさんは 1500＋300＝1800円 になります。
じゃあ最終的な２人の所持金の比は？　そうそう、これまた４：３なのです。

このことを当たり前だと感じてくれた人はどれくらいいるかな？
いまの例のように、ある決まった比（Ａ：Ｂ）の量に対して、同じＡ：Ｂの量を加えた場合、合計の量もＡ：Ｂとなり、このような性質を算数では加比の理と呼んでいます。
※たすのではなく、引いても同じことです

さて、このことを使って解く図形問題があります。いろいろなところですごく出題されますよ。必ず役に立ちますから、しっかり理解してくださいね！

下の図形において、ＥＧ：ＧＣを求めてください。

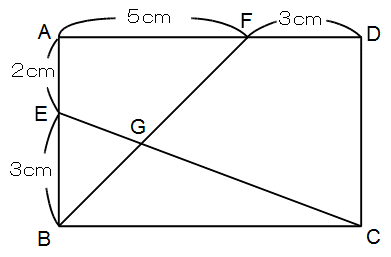
この問題で何回か使う図形の基礎知識を１つ確認しておきます。
高さが共通な三角形の面積の比は、底辺の比と等しい

△ＥＢＧと△ＧＢＣの底辺をそれぞれＥＧ、ＧＣとみると、２つの三角形の高さは共通です。
※ＢからＥＣに垂直に引く線が高さ
…とすると、ＥＧ：ＧＣの長さの比は△ＥＢＧと△ＧＢＣの面積の比と等しい。つまり、△ＥＢＧと△ＧＢＣの面積比がわかれば、ＥＧ：ＧＣが答えられるわけです。しかし残念ながら△ＥＢＧと△ＧＢＣの面積は簡単に求めることができません。

そこで、ＥとＦ、ＦとＣをそれぞれつないでみてください。
面積の比がＥＧ：ＧＣの比と等しくなる三角形が、また１組現れました。△ＦＥＧと△ＦＧＣです。しかしこれらの面積も簡単には求められません。

そしてここでいよいよ加比の理の登場です。
△ＥＢＧと△ＧＢＣの面積の比＝ＥＧ：ＧＣ
△ＦＥＧと△ＦＧＣの面積の比＝ＥＧ：ＧＣ　だったでしょう？

だったら、これらをタテに加えた面積の和もＥＧ：ＧＣの比になるはずです。
これぞ加比の理！

△ＥＢＧと△ＦＥＧを加えると△ＥＢＦ
△ＧＢＣと△ＦＧＣを加えると△ＦＢＣ になります。

こうしておくことで、△ＥＢＦや△ＦＢＣの面積が【底辺×高さ÷２】の公式で簡単に求められるのです。
△ＥＢＦ＝３×５÷２＝7.5cm²
△ＦＢＣ＝８×５÷２＝20cm²

少し説明に時間がかかりましたけど、ここで答えがわかりました。
ＥＧ：ＧＣの長さの比は、△ＥＢＦと△ＦＢＣの面積の比に等しく7.5：20
この比を整数の比に直して３：８が解答となります。

＊＊＊
加比の理を図形の問題に応用する考え方を理解してもらえたでしょうか。
図の中に、面積の比がＥＧ：ＧＣの比になる三角形が３組あって、その中で簡単に面積を求められるのが△ＥＢＦと△ＦＢＣという仕掛けでした。

また、上の問題は相似を利用するなど他の解き方もありますが、今回紹介した加比の理の考え方はすごくおもしろいし、必ず役に立つときがきますから、しっかりと覚えちゃってくださいね。

現在むかし書いたみんなの算数講座を少しずつ改訂中です。算数の内容に新しいも古いもないのですが、図形を作り直したり、古くなりすぎた雑談の内容などを取り替えています。ボクも改訂をがんばりますから、みなさんも算数がんばってくださいね。

ではまたどこかの講座でお会いしましょう！　風邪引かないでくださいね。