今回は、速さの問題の中から、意外と苦手な生徒が多い歩幅と歩数の問題を解説したいと思います。算数独特の考え方をするので、よく読んでしっかりマスターしてくださいね。


ではまず解説に協力してもらう登場人物の紹介から。

ガリバー　
ガリバー旅行記*に出てくるガリバーを想像してください。とにかくデカくて、ドシンドシンとごう音を響かせて歩きます。だけどその反面、動きはノロい。嫌われたりもするけど、ホントは心の優しい男なんだよね。
*紀伊国屋さんにリンクしておきます。角川書店から出てますね。この機会に読んでみるか〜という方はこちら

うさぎ
♪う〜さぎお〜いし、か〜のやま〜♪のうさぎです。　童謡ふるさとを聞く
くだらない話ですが、ボクは小さい頃、うさぎがおいしいのかと本気で思ってました。「おいし」が「美味しい」ではなく「追いし」つまり追いかける意味だと知ったのは、確かハタチに近いトシの頃だったと思います。え？あなたも勘違いしていた？　同じ思い込み仲間、うれしいですね（笑）

ではここで問題を出します。

今でもよく見かけますね、この問題は。
塾のテキストや参考書では「歩幅と歩数の問題」といわれますが、私の授業ではガリバー問題です。ガリ、と言いかけた瞬間に、ボクの生徒なら口をそろえて「あぁ、アレね」
そういえば今までこうした問題のネーミングをいくつしたかなぁ。数え切れない…　でも楽しいネーミングがあるほど、生徒はずっと忘れないみたいですよ。

少し言葉の説明をしておきましょう。

歩幅
１歩の長さのことです。
等しい距離を進むのにＡ歩とＢ歩かかる場合では、歩幅の比はＢ：Ａ（逆比）になります。
上の問題では、ガリバーが２歩で進む距離をうさぎは30歩。歩幅が長いのは当然ガリバーです。

歩数
等しい時間内に何歩進めるか？
俊敏性（しゅんびんせい・動きのはやさ）と考えてください。ガリバーよりうさぎの方が断然すばしっこいでしょう？
うさぎは歩幅は短いですが動きでは勝（まさ）りますから、ガリバーがノロノロ歩いているうちに、どんどん歩くことができるわけです。歩幅ではガリバーの勝ちですが、歩数ではうさぎの勝ちですね。

では、上の問題で歩幅の比、歩数の比を考えてみましょう。

歩幅の比
等しい距離をガリバーは２歩、うさぎは30歩かかるから、
歩幅の比は、数値を逆にして　ガ：う＝30：２＝15：１

歩数の比
等しい時間内に、ガリバーは６歩、うさぎは110歩進むから、
歩数の比は、ガ：う＝６：110＝３：55　（逆にしません）

ガリバーとうさぎでは、その体の大きさを考えても、１歩の歩幅はガリバーが大きいに決まっています。これが歩幅の比。
しかし、どちらがより動くかといえば、これは圧倒的にうさぎでしょう。
こちらが歩数の比。

ガリバーとうさぎの速さの比を考えるときは、歩幅と歩数の両方を合わせて考えなくてはなりません。こうして次の公式が登場します。

（速さの比）＝（歩幅の比）×（歩数の比）

実際に計算してみます。
ガリバーとうさぎの歩幅の比は15：１、歩数の比は３：55だから、
ガリバーとうさぎの速さの比は（15×３）：（１×55）
=45：55＝９：11 …(1)の答え
歩幅のハンデを歩数で逆転して、うさぎの方が速いですね。

次に問題(2)の解説です。

先にガリバーが10歩進んでいます。その距離をうさぎが追いかけていくと、うさぎがガリバーを追いかけ始めてから追いつくまでに両者が進む時間は同じだから、両者が進む距離は速さの比と同じで９：11になります。（下図、青い線の部分）
重要　等しい時間で進む距離の比は、速さの比と等しい



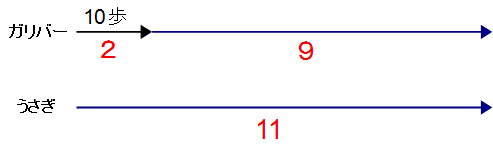
上の図のように、うさぎがガリバーを追いかけ始めてから追いつくまでに、ガリバーの進んだ距離を９とすると、うさぎの進んだ距離は11です。

このことから、ガリバーが先に進んだ10歩分の距離が11−９＝２にあたることがわかり、
１にあたる距離を10歩÷２＝ガリバーの５歩分、
11にあたる距離を５歩×11＝ガリバーの55歩分と計算することができます。

問題で求めるのは、11の距離（ガリバーの55歩分）をうさぎが何歩かかるか？だから、最後にもう一度歩幅の比（ガリバー：うさぎ＝１：15） を利用して、
55×15＝825（歩）が正解となります。…(2)の答え
※55歩と答えてしまう誤答がよくあります。11の距離はガリバーなら55歩ですが、うさぎだとその15倍の歩数が必要です。だってガリバーが１歩で進む距離をうさぎは15歩で進むのですから。

＊＊＊
歩幅と歩数のガリバー問題。いかがでしたか？
歩幅と歩数をかけて速さの比を作ることが最初のポイントです。(2)ではどちらの歩数で求めるのかを勘違いしないでほしいですね。

ではみなさん今回はここまでです。次回の講座でまた算数を楽しみましょう！

カーテンコール
しかしうさぎがおいしいとはかわいそうな思い込みでした。ごめんなさい。わが国ではうさぎはかわいいし食べません。but 諸外国では普通に食用もあるそうです（本当）