今回の第19講座は、ある 速さの問題 に２つの有力な解き方があり、みなさんはどちらが好きでしょうか？というアンケートをかねた講座です。ボクの意見は最後に書きますね。


２つの有力な解法がある速さの問題。それはこんな問題です。

では有力といった２つの解法を１つずつ紹介します。

解法１　面積図を利用
次のような面積図を書いて解きます。
面積図とは、２つの量の積を面積によって表現する算数用ツールです。〈タテ〉×〈横〉が長方形の面積になるのと同じように、速さの問題なら〈速さ〉と〈時間〉をかけた〈距離〉が面積になります。



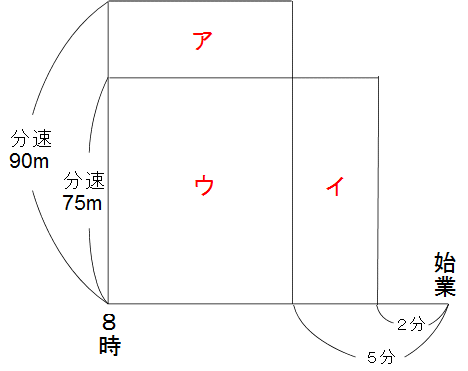
面積図のタテが速さ、横が時間の経過です。
「分速90ｍで行くと 始業５分前に着く」
「分速75ｍで行くと 始業２分前に着く」
この２つの条件を、長方形を重ねて書くことで表現します。

学校までの距離は変わらないから、重なっている２つの長方形の面積は等しく、共通しているウを取り去ることで、アの面積とイの面積が等しいことがわかります。

イの面積＝75×（５−２）＝225　→アの面積も225
アの横の長さ　225÷（90−75）＝15
よって、分速90ｍで行くと15分かかることがわかり、
始業時刻は ８時＋15分＋５分＝８時20分
家から学校までの距離は 90（ｍ／分）×15分＝1350ｍ
無事に解答が求められました。


解法２　比を利用
６年生（塾によっては５年生）になって比が使えるようになれば、面積図を使わないこちらの解法も考えられます。

では解説します。

家から学校までの距離は変わらないので、２つの行き方では速さの比と時間の比が逆の比になります。

重要　距離が一定のとき、速さの比と時間の比は逆の比になる

分速90ｍで行った場合と分速75ｍで行った場合の速さの比は
90：75＝６：５
所要時間の比は逆の比になって５：６です。

所要時間の差は ３分（５分−２分）で、これが６と５の差の１にあたるから、５にあたる時間（分速90ｍで行ったときの所要時間）は３分×５＝15分

家から学校まで15分で着いて始業時刻の５分前だから、
学校の始業時刻は ８時＋15分＋５分＝８時20分
学校までの距離は 分速90ｍ×15分＝1350ｍ
と求めることができます。

＊＊＊
さて、みなさんはどちらの解法を支持したいと思いますか？
ボク自身、中学受験の算数を教え始めて20年以上たちますが、これをどちらで教えるかはいまだに悩ましいです。答えが出ません。

みなさんの頭になじみやすい方で解いてもらえばよいと思う気持ちもありますが、受験に向けていろいろな算数の問題に対応していくためには、解法のポケット（引き出し）は多い方がよいというのも事実です。

自分の家で塩味の卵焼きばかり食べていて、あまり卵焼きを好きになれなかった子供が、あるとき友だちの家で砂糖味の卵焼きを食べ、
「卵焼きって、こんなに美味しい食べ物だったのか〜」と感激した.....
ボクの師匠がよく父母会で使っていたたとえ話ですが、算数をなかなか好きになれなかった子供が、ある問題の ある解法をすごく気に入って、それをきっかけに算数への興味が広がり、成績がどんどん伸びていったというケースもあります。だから本音をいえば、両方を使えると素晴らしいのではないかと思います。
もちろん勉強には時間の制約もありますから、理想ばかりを言っていられないのですが、いろいろな解き方を使えるようになることが、算数成績アップの助けになることだけは間違いないでしょう！

あとがきが長くなりました。それではみなさん、また次回の講座でお会いいたしましょう。
もしよかったらアンケートの回答をトップページのメールフォームから送ってくださいね。