今回の講座では、水の入った容器に角材をつっこんでいくときの水深変化を考えます。角材つっこみ問題と言われてますね。お風呂に入ったときを思い出してくれると説明がしやすくなります。


水が（お湯か...）入っているお風呂の湯船にあなたが入ると、お湯の深さは上がりますね？
あるいは湯船が満たされて外にこぼれるかもしれませんが、上がったりこぼれたりしたお湯の体積は、あなたのカラダ全体の体積ではなく、あなたのカラダの中で水面より下にあるパーツの体積と等しいです。　パーツ…足とか胴体とか
　
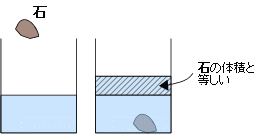
そのことからもわかるように、水の入っている容器に何かを入れると、何かが水面より下に入った分だけ水の深さが上がります。

では前置きはこのヘンにして問題にいきましょう。

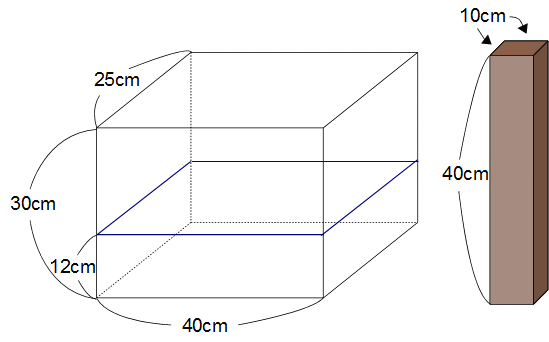
下の図左のようなタテ25ｃｍ、横40ｃｍ、高さ30ｃｍの直方体の容器があり、12ｃｍの深さまで水が入っています。 いま、タテ、横10ｃｍ、高さ40ｃｍの角材（下の図右）を、底面が容器の底面と平行になるように水の中へ入れていきます。 (1)水面が１ｃｍ上がるまで角材を入れたとき、角材の底面は容器の底面の何ｃｍ上にありますか？ (2)角材の底面が容器の底面につくまで入れたとき、 水の深さは何ｃｍになりますか？

塾などで習ったことある人なら「あぁコレね」という感じでしょうけど、そうでない人たちにとっては、あまり見覚えのない問題だと思います。
こうした問題は、立体を平面におきかえた図で考えることが重要です。いちいち立体の図を書くのは大変ですからね。ぜひ覚えておいてください。

重要　棒突っ込み問題は立体のままで考えず、正面からみた平面図で考える

(1)


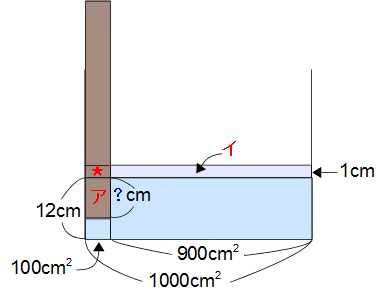
上の図の横線は容器や角材の底面積を表し（長さではありませんよ）タテ線が高さを表しています。すると図の面積が体積を表すことになりますね。　底面積×高さ＝体積

容器全体の底面積＝25×40＝1000ｃｍ^２
角材の底面積 ＝10×10＝100ｃｍ^２より、その差は 1000−100＝900ｃｍ^２ です。

角材の突入によってアの部分の水が押しつぶされ、イの部分に移動します。湯船にからだをつけたとき、湯面が上昇するのと同じ理屈です。
つまり、アの部分とイの部分の体積が等しいことになりますね。
（★の部分にはもともと水がないから、アにもイにも★の部分は入れません）

イの部分の体積＝ 900×１＝900ｃｍ^３
アの部分の高さ（？ｃｍ）＝900÷100＝９ｃｍ

したがって容器の底面から角材の底面までの長さは、12−９＝３ｃｍ とわかります。

(2)


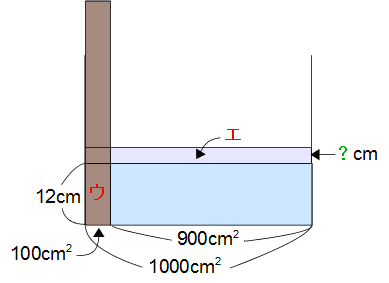
角材の底面が容器の底面につくまで入れると、上の図のようになります。
ウの部分の水がエの部分に移動しますね。
ウの部分の体積＝100×12＝1200ｃｍ^３
エの部分の高さ（上昇分？ｃｍ）＝1200÷900＝1200/900＝4/3ｃｍ＝１と1/3ｃｍ
よって、角材突っ込み後の水の深さは12＋１と1/3＝13と1/3ｃｍとわかります。

＊＊＊
いかがでしたでしょうか？　角材つっこみ問題を楽しんでもらえましたか？
じつは今回の問題はまだ基本問題で、なかにはもっと複雑な問題もあります。容器に穴があいていたり、突っ込む物体がものすごい形をしていたり…。あふれて水がこぼれてしまうというパターンもありますよ。
そうした問題はまたいつかどこかで書くとして、今回おさえてもらいたいポイントは、
水面下に沈んだ物体の体積の分だけ水面が上昇するというごく自然なことです。あとは〈最初の水面〉と〈つっこみ後の水面〉を間違えないようにね。

では今回はこんなところで終わりましょう。次回の講座も期待していてください！