今回の第21講座では、集合（しゅうごう）の内容から、3つの輪が重なるベン図の考え方を解説します。2つの輪は簡単なのですが、3つになると意外な盲点（もうてん）があります。よく読んで知識を増やしてください。


算数や数学で勉強する「集合」とは、同じ性質をもったいくつかのものの集まりのことです。
※算数では「集合」のことを「集まり」といいますが、ここでは「集合」と呼ぶことにします。

たとえば1ケタの素数の集合といえば{2、3、5、7}
24の約数の集合といえば{1、2、3、4、6、8、12、24}などです。

そして、いくつかの集合の関係を考えるとき、左のようなベン図と呼ばれる図を用意すると、問題の内容が整理され、とてもわかりやすくなります。
おそらく2つの輪のベン図については経験のある人が多いと思いますから、今回の講座では3つの輪のベン図を使う問題について説明することにします。

たとえば次のような問題です。

目が回ってしまいそうな条件の多さです。さすがに頭の中だけでは整理しきれないでしょう？
ではさっそく３つの輪のベン図を使って、問題を整理してみましょう。


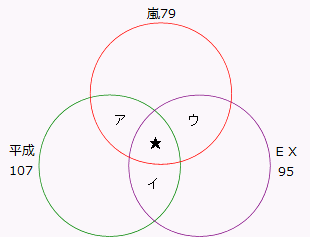
←このようなベン図になりますね。
では解説を始めます。

誰も選ばなかった人はいないから、左のベン図の
合計は小学生の人数の150人です。
嵐を選んだ79人、平成ジャンプを選んだ107人、
EXILEを選んだ95人をすべて加えると、
79＋107＋95＝281人

たし算の結果が小学生の150人を超えてしまっています。それは重なったところをダブって数えているからです。ダブって数えているところは次のようになっています。

ア…嵐の○と平成の○で２回数えている　（１回よぶん）
イ…平成の○とEXの○で２回数えている（１回よぶん）
ウ…嵐の○とEXの○で２回数えている　（１回よぶん）
★…すべての輪○○○で３回数えている　（２回よぶん）

つまり、さきほどの合計の281人は、
ア、イ、ウを１回ずつと★を２回、よぶんに数えているのです。
そこで、よぶんに数えた人数を次のように計算します。

問題の条件から、
ア＋★＝48人　イ＋★＝60人　ウ＋★＝51人
これらをすべて加えて、
（ア＋★）＋（イ＋★）＋（ウ＋★）
＝48＋60＋51＝159人　←ア＋イ＋ウ＋★＋★＋★

この人数を最初に合計した281人から引いてみます。
281−159＝122人

この引き算によって、1回ずつよぶんだったア、イ、ウはうまく消すことができましたが、2回よぶんだった★を3回引いたから1回引きすぎていることになります。
※少し前の下線を引いた式を見てください。159人は★が3回ふくまれてます。ダブりを消すためには、★の人数は2回分引けばいいので、3回分引いてしまったら1回分引きすぎですね。

そこで、122人に★を1回分をたせば、小学生の人数の150人になるはずです。
122＋★＝150より、★＝150−122＝28人
これが全部のグループを選んだ人の人数です。

＊＊＊
3つの輪が重なるベン図の問題、理解できたでしょうか？

3つの輪のベン図では
a)3つの輪をすべて合計し
b)そこから2つの輪の重なりをすべて引き
c)最後に3つの輪の重なりを1回分たすと
ダブりをのぞいた全体の人数を求めることができます。このことは覚えておくと便利ですよ！

今回の改訂で、問題に登場していただく芸能人を変えました。そういえば 安室ちゃん や あみーご（鈴木あみさん）に登場してもらっていたんだなーと、この講座を最初に書いた頃をとても懐かしく思い出しました。
嵐、平成ジャンプ、EXILE。みなさんはベン図のどこに含まれる人でしたか？
このアンケート結果はおかしいよ、というご意見もおありでしょうが、まぁ算数の例題なんで、実際の人気を示していなくても許してくださいね。

それではみなさん、次回の講座と今回登場してもらったグループの活躍を期待してください！