今回は東京の中心部をグルッと一周している山手線（やまのてせん）をもじって、円が図形の辺に沿って外側や内側を一周する山手円（やまのてえん）の講座です。外回りも内回りも事件はカドで起こります。


まぁ本題にはあまり関係ないんですが、一応タイトルにお借りした関係で、山手線の外回りと内回りのイラストを貼っておきますね。外回りと内回りがどっちなのかは確かにまぎらわしいのですが、電車もクルマと同じで左側通行と覚えるのだそうです。お借りしてきたイラストですがとてもわかりやすいですね。　参考サイト



さて、では本題へ入ります。こんな問題がよくありますよね。

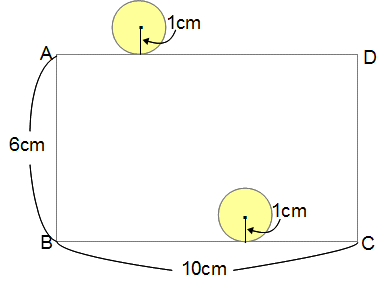
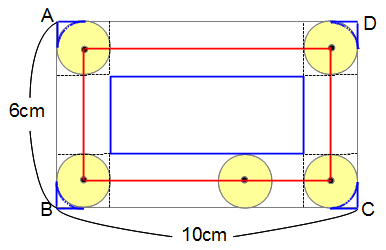
タテ6cm、ヨコ10cmの長方形があります。 この長方形の辺にそって半径１cmの円が一周します。 １．円が長方形の外側を一周するとき、 (1)中心が動く線の長さは何cmですか？ (2)円が通過する部分の面積は何ｃｍ２ですか？ ２．円が長方形の内側を一周するとき、 (1)中心が動く線の長さは何cmですか？ (2)円が通過する部分の面積は何ｃｍ２ですか？

では１つずついきましょう。

１．外回りの(1)中心の動きから。

下の図を見てください。
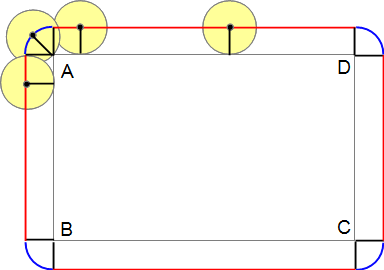
円が長方形の辺に沿って外側を回るとき、中心の動きは長方形の辺に平行な直線部分（赤線）と、長方形のカドのところでカーブになる部分（青線）に分かれます。
作図のコツとしては、長方形のカドに半径と等しい棒（黒太線）を垂直に立て、辺に平行な直線と、カドのところはおうぎ形を書いてつなげばよいと思います。

直線部分…６×２＋10×２＝32cm
おうぎ形の弧の部分…４つ合わせると半径１cmの円周です。１×２×3.14＝6.28cm
これらを合計して、求める解答は38.28cmです。



次に(2)の円が通過する部分の面積です。
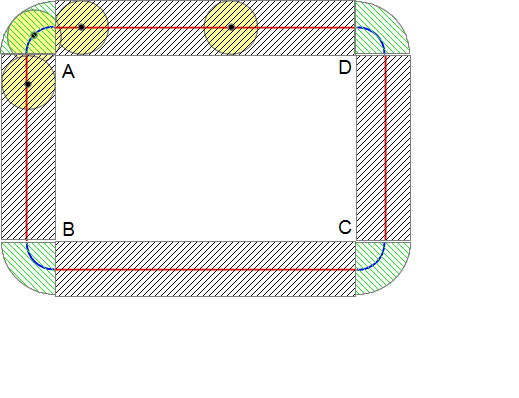
円が通過する部分は、下の図のように、長方形の辺に沿った部分は長方形、カドは90°のおうぎ形になります。
作図のコツは、円の直径の幅まで広げるように長方形とおうぎ形を書けばよいでしょう。

長方形部分…タテ２cmヨコ10cmの長方形が２つ、タテ６cmヨコ２cmの長方形が２つです。
２×10×２＋６×２×２＝64cm²
おうぎ形部分…４つ合わせると半径２cmの円です。２×２×3.14＝12.56cm²
これらを合計して、求める解答は76.56cm²です。


さて、(1)と(2)の解答を見て何かお気づきになりませんか？
このことはトップページの公式テクのおみやげコーナーにも書いていますが、(1)で求めた中心の動く線の長さに円の直径をかけると、円が通過する部分の面積になるのです。これは外回りのマル秘公式でセンターラインの公式と呼ばれてます。※内回りでは使えません
長方形部分では当たり前に思えるかもしれませんが、おうぎ形部分でも青線×円の直径＝緑の斜線のおうぎ形の面積になるのです。ここでは深入りしませんが、興味のある方は理由を考えてみてください。

＊＊＊
続けます。今度は内回りです。

２．(1)中心の動き。
内回りの中心の動きは簡単です。長方形の四隅に円を書き、その中心をつないだ直線（赤線）になります。タテ線が６ー１×２＝４cm、ヨコ線が10ー１×２＝８cmです。
解答は４×２＋８×２＝８＋16＝24cmです。

(2)円が通過する部分の面積。
これは逆に円が通過しない部分を考えて、長方形ＡＢＣＤ全体から引けばよいでしょう。
円が通過しない部分は
〈中央にある青線で示した長方形の内部〉と〈長方形ＡＢＣＤのカドの部分〉です。中央は忘れないと思いますが、カドの部分をうっかり忘れる人が多いので気をつけてください。

青線で示した長方形…タテ２cm、ヨコ６cmです。２×６＝12cm²
カドの部分…４つ合わせると、１辺２cmの正方形から半径１cmの円を引いた図形になります。
２×２ー１×１×3.14＝４ー3.14＝0.86cm²

これらの通過しない部分を全体の長方形ＡＢＣＤから引いて、
円が通過する部分の面積は
６×10ー（12＋0.86）＝60ー12.86＝47.14cm²と求めることができます。


いやいや長くなりまたね。だいぶ長いこと欠番になっていた第22講座が書き直せてホッとしています。
外回りと内回りだから　やまのてせん　をもじって　やまのてえん　というタイトルにしただけです。それ以上の意味はないですけど、みなさんの中で思い出になってくれたらとてもうれしいですよ。

ではこれにて　やまのてえん講座は終講。また次の講座でお会いいたしましょう！