今回の講座はニュートン算の解説です。豊島区のＫ・Ｔさんから、お嬢さんがわからなくて困っているからと、講座のリクエストがありました。わかってもらえるようにがんばって書こうと思います。

ニュートン1642-1727
イングランド 科学者 哲学者
ニュートン算とは、
もともと ある決まった量 があり、その量を減らしていくときに、同時に増える量も発生してくる問題のことです。
昔、ニュートンがこの問題を出したことから、ニュートン算という名前がつけられています。ニュートンは算数もすごく得意だったようですね。
よく出題されるパターンは、今回紹介する「泉の水をポンプでくみ出す問題」「牛が牧草地の草を食べる問題」「売り場の行列と窓口の問題」などがあります。

では問題を出してみます。

下のような線分図を書いて考えます。
　
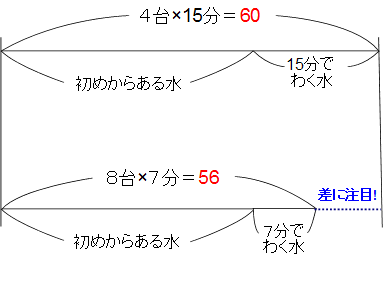
泉には初めからたまっている水があります。〈初めからある水〉と呼びましょう。
泉の水をポンプでくみ出すとき、くみ出している間も水はわいてきますから、
〈くみ出す水〉は、〈初めからある水〉＋〈あとからわく水〉です。

〈くみ出す水〉については、
ポンプ１台が１分でくみ出す量を１台×１分＝１と考えてください。
４台×15分＝60、８台×７分＝56です。
※この赤い数字の量は無単位で考えてよいでしょう。

２つの線分図の差に注目してください。
15−７＝８分で〈あとからわく水〉水が60−56＝４にあたります。
すると１分で〈あとからわく水〉は４÷８＝0.5
したがって、〈初めからある水〉は60−0.5×15分＝52.5とわかります。

ここまでが準備段階で、次のことがわかりました。
〈初めからある水〉＝52.5
〈くみ出す水〉＝１　※１分あたり
〈あとからわく水〉＝0.5　※１分あたり

さて初めからある52.5の水を５分でくみ出すためには、
１分あたり 52.5÷５＝10.5 の水を減らせばよい（くみ出す ではない）のですが、
１分あたり0.5の水がわいてしまうので、その分を加えて考えると、
１分で10.5＋0.5＝11 の水をくみ出す必要があります。
※１分で11の水をくみ出せば、0.5の水がわいてきても10.5の水が減るということです

ポンプ１台が１分でくみ出す水の量が１だから、１分で11の水をくみだすには
11÷１＝11より、11（台）のポンプが必要です。

＊＊＊
以上、ニュートン算の解説でした。
最大のポイントは、
〈くみ出す水〉の量を、ポンプの台数とくみ出す時間をかけて表現する
ところでしょうか。

確かにその点は他の文章題ではあまり用いない〈無単位の量を作って考えるというテクニック〉が必要ですが、そこをニュートン算の特長と理解してクリアーすることができれば、それほど難しい文章題ではないと思います。
ニュートン算が苦手な人は、どこかで難しく考えすぎて、迷路に迷い込んでしまうことが多いようです。今回の講座を参考に、しっかり線分図を書いて落ちついて解くようにしてくださいね。

Ｋ・Ｔさん、これでわかってくれるかな？
それではみなさん、また次回の講座でお会いしましょう。さようなら。

※この講座で取り上げてほしいテーマがありましたらメールなどでお知らせください。必ず採用するお約束はできませんが、みなさんのリクエストにはなるべくこたえていきたいと思っています。