 今回はN角形の公式たちです。受験で使うのは〈N角形の内角の和〉〈正N角形の1つの内角〉〈N角形の外角の和〉〈N角形の対角線の総数〉といったところでしょうか。これらはさすがに覚えておかないと戦えませんよ。 今回はN角形の公式たちです。受験で使うのは〈N角形の内角の和〉〈正N角形の1つの内角〉〈N角形の外角の和〉〈N角形の対角線の総数〉といったところでしょうか。これらはさすがに覚えておかないと戦えませんよ。
それではまずN角形の公式を紹介です。どれも頭にたたきこんでください。
理由はあとで説明します。
| 求めるもの |
公式たち |
| N角形の内角の和 |
180×(N−2)°…A |
| 正N角形の1つの内角 |
(A÷N)° ※他の手もある |
| N角形の外角の和 |
360° ※一定値 |
| N角形の対角線の総数 |
N×(N−3)÷2 本 |
使い方の例
五角形ならN=5、六角形ならN=6のように、Nにあてはめて計算します。
外角の和は一定の値だから計算する必要がありません。
※外角の和は十五角形でも六十角形でも360°で変わりません。
(例)八角形の内角の和 180×(8−2)=180×6=1080°
(例)正八角形の1つの内角 1080÷8=135°
(例)八角形の対角線の総数 8×(8−3)÷2=8×5÷2=20本
では、いまの公式を使って計算した三角形〜十二角形の一覧表をどうぞ。こういう一覧表、ありそうであまりありませんよね。
ボクは十二角形で断念しましたが、がんばり屋さんで努力できる人は、ぜひもう少し下まで続けてみてください。何角形まで続けたらギネスブックに乗るかな???(冗談)
| |
内角の和
|
外角の和
|
正多角形の
1つの内角
|
対角線
の総数
|
| 三角形 |
180° |
360° |
60° |
0本 |
| 四角形 |
360° |
90° |
2本 |
| 五角形 |
540° |
108° |
5本 |
| 六角形 |
720° |
120° |
9本 |
| 七角形 |
900° |
128と4/7 ° |
14本 |
| 八角形 |
1080° |
135° |
20本 |
| 九角形 |
1260° |
140° |
27本 |
| 十角形 |
1440° |
144° |
35本 |
| 十一角形 |
1620° |
147と3/11 ° |
44本 |
| 十二角形 |
1800° |
150° |
54本 |
さて大事なのは、いまの公式たちの根拠ですね。ではそれぞれの理由を説明していきます。
N角形の内角の和について
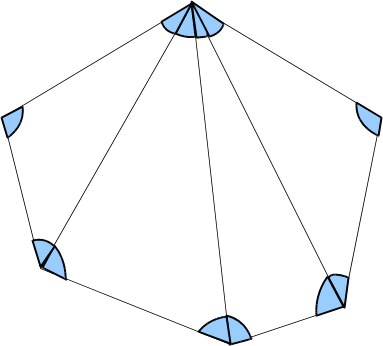
左の図は六角形を4つの三角形に分割した様子ですが、このように
N角形は必ずN−2(個)の三角形に分割
することができて、
三角形の内角の和は180°だから、
N角形の内角の和は180×(N−2)°になります。
正N角形の1つの内角について
正N角形はすべての角の大きさが等しいN角形だから、内角の和180×(N−2)°をNで割ればよいですね。
N角形の対角線の総数について
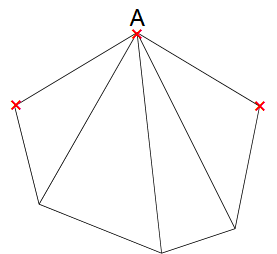
左の図の六角形で、1つの頂点Aに集まる対角線は3本です。
頂点Aから両隣りの頂点と自分自身の3ヵ所には対角線が引けません(×印) このように
N角形は1つの頂点にN−3(本)の対角線が集まっていて、これに頂点の数NをかけるとN×(N−3)
このままだと往復する対角線をダブッて数えているから
N角形の対角線の総数はN×(N−3)÷2 本です。
N角形の外角の和について
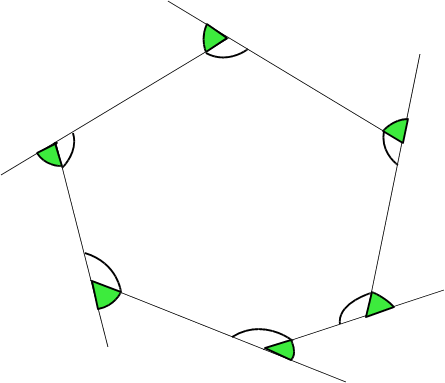
外角というのは、内角を180°に延長した外側の角(緑色の角)のことを指します。
上の図の六角形の場合では、6つの頂点に6本の直線があり、合計すると180×6=1080°です。ここから六角形の内角の和720°(白い角の合計)を引くと、1080°−720°で外角の和は360度になります。
N角形の場合でも180×N−180×(N−2)という式ができて、この式はNコの180°から、Nより2コ少ない180°を引いているから、180°が2コ残って360°となります。
したがって外角の和は何角形であっても一切変わることがありません。
以上で公式の理由の説明を終わりますが、最後にもう1つオマケを追加します。
正N角形の1つの内角についてですが、内角の和を求めてNで割るという方法以外に、外角の和(360°)をNで割って1つの外角を先に求め、それを直線の180°から引くという方法もあります。これを正N角形の1つの内角を求める〈第二公式〉ということにして、今回の講座をお開きにしようと思います。この講座で解説した内容はいつまでも忘れないでくださいね!
正N角形の1つの内角〈第二公式〉180−360÷N(°)
それではみなさん、また次の講座でお会いいたしましょう。元気でね!さようなら。
カーテンコール
タイトルの「Nの悲劇」ですが、NはもちろんN角形のN。悲劇はこれを知らなかったら悲劇だゾの悲劇です(笑)読書不足の最近の子供たちにエラリークイーン不朽の名作のタイトルを知ってほしかったという意味もあります。Wの悲劇、Xの悲劇、Yの悲劇etc みなさん、いつか読んでみてくださいね!
|

 今回はN角形の公式たちです。受験で使うのは〈N角形の内角の和〉〈正N角形の1つの内角〉〈N角形の外角の和〉〈N角形の対角線の総数〉といったところでしょうか。これらはさすがに覚えておかないと戦えませんよ。
今回はN角形の公式たちです。受験で使うのは〈N角形の内角の和〉〈正N角形の1つの内角〉〈N角形の外角の和〉〈N角形の対角線の総数〉といったところでしょうか。これらはさすがに覚えておかないと戦えませんよ。

