|
 ����̍u���͗��̐}�`�ł��B�e�[�}�́A�����̂̑̐ς��Œ肵���Ƃ��A�\�ʐς��ǂ̂悤�ɕω����邩�̒����ł��B�̐ς������ł���������̋���͂����Ԃ�������ł���ˁB ����̍u���͗��̐}�`�ł��B�e�[�}�́A�����̂̑̐ς��Œ肵���Ƃ��A�\�ʐς��ǂ̂悤�ɕω����邩�̒����ł��B�̐ς������ł���������̋���͂����Ԃ�������ł���ˁB
�����͏���������������c�B
�C���^�[�l�b�g��ɐ��̐��قǂЂ��߂������T�C�g�̒�����A�����̃T�C�g���������������Ă��邱�Ƃ��ƂĂ����ꂵ���v���܂��B
�{�N�̃z�[���y�[�W�^�c��10�N���܂������A��͂萯�̐��قǑ������ł��̂ŁA�z�[���y�[�W���`����̂̓z���g����ł��B�Z����艽�{�����...�@
��`����ɂ͉��������Ă�Google��yahoo!�̌����G���W�����������Ȃ��ƂȂ�Ȃ��̂ł����A�ނ�ɕ]�����Ă��炤���Ƃ͕����ł͂Ȃ��ł��B����͌l���x���̘b�ł͂Ȃ��A��������̉�Ђ₨�X�ł���J���Ă��邱�Ƃł��傤�ˁB���������ӂ��ɂ������ʂɕ\�������Ƃ������Ƃ��n�b�L�����Ȃ��̂ł���B�����Ƃ����̂�������n�b�L�������Ă��܂��ƁA����ɑ������u�����T�C�g���肪��ʂɂȂ��Ă��܂��A�����҂�]�݂̃T�C�g�ɗU������Ƃ��������G���W���̈Ӗ�������Ă��܂��̂�������܂��ǂˁB
�����܂���A���������̂��肪�E�����Ă��܂��܂����B
���̃z�[���y�[�W�ł͂��ꂩ����y�����a�₩�ɖ��ɗ��Z������葱�������Ǝv���܂��B�����������C�ɓ����Ă��ꂽ��A�F������m�荇���̐l�ɂ������Ă����Ă��������ˁB��ԑ�Ȃ݂̂͂Ȃ����l�ЂƂ�̋M�d�ȃA�N�Z�X�B���ꂾ���͊ԈႢ�Ȃ��Ǝv���Ă��܂��B
����A�Ȃ�������???
�������A���̂̍u�����������Ƃ��Ă܂�����B�������������Ƃ��������Ƃ����璲�q��������Ă��܂��܂���...
�i�[�ċz�j
�ł͖{��̎Z���u���B���̏Љ�ł��B
�P�ӂ̒������P�����̗����̂�24����܂��B
������ςݏd�˂Ă��낢��ȑ傫���̒����̂����Ƃ��A�\�ʐς������Ƃ��������Ȃ�̂͂ǂ̂悤�Ȑςݕ��������ꍇ�ł��傤���H
|
�����̂�ςݏd�˂Ē����̂����Ƃ��A�ł��オ�钼���̂ɂ̓^�e�A���A�����̂R���������邩��A�e�����̌������A���A���Ƃ���ƁA���~���~����24���Ƃ����������܂��B
���ȉ��A���A���A���ƃ^�e�A���A�����̑Ή��͓��ɏd�v�ł͂���܂���B�R�����̌��̑g�����������Ȃ�A�^�e�A���A�����œ��ꂩ��肪�����Ă������`�̒����̂��ł��邩��ł��B
| |
���� |
���� |
���� |
| A |
�P |
�P |
24 |
| B |
�P |
�Q |
12 |
| C |
�P |
�R |
�W |
| D |
�P |
�S |
�U |
| E |
�Q |
�Q |
�U |
| F |
�Q |
�R |
�S |
���A���A���̌��͐����ł����A�R�̐����̐ς�24�ɂȂ�̂�
�������̃p�^�[�������肻���ł��B
�����������̂悤�ɑ召�W�����߂Ē��ׂ�ƁA���\�̂U�̃p�^�[�������邱�Ƃ��킩��܂��B
���āA�����R�����̌��ƕ\�ʐςɂǂ̂悤�ȊW�����邩���v�Z���Ē��ׂĂ݂܂��傤�B
���ȉ�������ł͂R�����̌������~���~���ƕ\�L���܂��B
�\�ʐς̌v�Z���@�́A���̂Q���l������Ǝv���܂��B
�@�����̂̕\�ʂɂ́q�R��ނ̒����`���Q�����r����ƍl���Čv�Z����B
�����̂̕\�ʐρ��i���ā~���{���ā~�����{���~�����j�~�Q
�A�S������24�̕\�ʂɂ��鐳���`�̖����i24�~�U��144���j����A�ڒ��ɂ���ĉB��鐳���`�̖����������Čv�Z�����B
���A�͂�����Ɩʓ|�B���ʂ͇@�ł��傤�B���������̍u���ł͇A���l���Ă݂܂��B
�p�^�[���`
�P�~�P�~24�̏ꍇ�ł��B
���̐}�̂悤�ɂP�����ɃY���Y���ƕ��Ԗ_��̒����̂ɂȂ�܂��B
�@�̕��@�ŕ\�ʐς��v�Z����ƁA
�i�P�~�P�{�P�~24�{�P�~24�j�~�Q��98����2�ƂȂ�܂��B
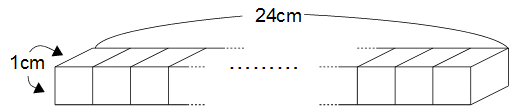
�ǂ������ꂪ�ŏ��̕\�ʐςł͂Ȃ������ł��B�݂Ȃ�������������܂��H�@���̕��ו����ƕ������肪�ƂĂ��������ł��ˁB
�p�^�[���a�͊��������p�^�[���b�ł��B
�p�^�[���b
�P�~�R�~�W�̏ꍇ�ł��B
���̏ꍇ�̕\�ʐς́i�P�~�R�{�P�~�W�{�R�~�W�j�~�Q��70����2�@�ƂȂ�܂��B
�p�^�[���`���͌���܂������A�\�ʐς͂܂��������ł������ł��B
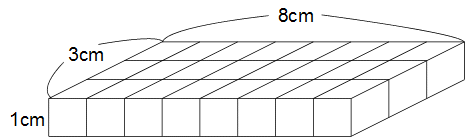
���̓p�^�[���d�ׂĂ݂܂��傤�B
�p�^�[���d
�Q�~�Q�~�U�̏ꍇ�ł��B
���̏ꍇ�̕\�ʐς́i�Q�~�Q�{�Q�~�U�{�Q�~�U�j�~�Q��56����2�@�ƂȂ�܂��B
�p�^�[���b��肳��Ɍ���A�����ԕ\�ʐς��������Ȃ��Ă��܂����B
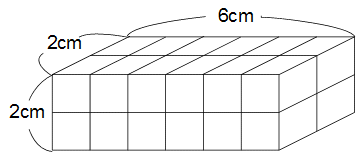
�Ō�Ƀp�^�[���e�ł��B
�p�^�[���e
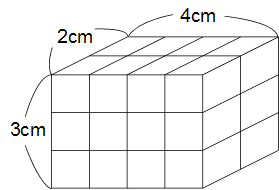
�Q�~�R�~�S�̏ꍇ�ł��B
���̏ꍇ�̕\�ʐς́i�Q�~�R�{�Q�~�S�{�R�~�S�j�~�Q��52����2�@�ƂȂ�A
���̐ςݏグ���������ꍇ���\�ʐς��ł��������Ȃ�܂��B
���Ă݂Ȃ���͂����܂ł̌����ŁA�R�����̌��ƕ\�ʐςɉ��������ł��܂������H
���́A�̐ς̌��܂��������̂̕\�ʐς����������邽�߂ɂ́A�Ȃ�ׂ������̂ɋ߂��`�ɐςݏグ��悢�̂ł��B
����͂����ق���������~���~����24�Ƃ������ŁA�ς�24�ɌŒ肵���܂܁��{���{���̘a���Ȃ�ׂ������������ƍl���邱�Ƃ��ł��܂��B
���ɂ܂Ƃ߂̕\������܂�����A���{���{���̒l���m�F���Ă݂Ă��������B�p�^�[���`��26���ő�ŁA�ȉ����X�ɘa���������Ȃ��Ă����A�p�^�[���e�̂X���ŏ��̘a�ɂȂ��Ă��܂��B
���Ęb�����тĂ��܂��܂����A�ł͂ǂ����ĂȂ�ׂ������̂ɋ߂��`�ɐςݏグ���Ƃ��A�\�ʐς��ł��������Ȃ�̂ł��傤���H
����́A�Ȃ�ׂ������̂ɋ߂��`�ɐςݏグ�������A�����̂ǂ����̐ڒ��ӏ��������Ȃ�����ł��B�����قǁ@������Ɩʓ|�@�Ə������A�̍l�����ł��B
�S������24�̕\�ʂɂ��鐳���`�̖�����24�~�U��144���ł��B
�p�^�[���`�̗��̂ł́A�����̂ǂ����̐ڒ��ӏ���23��������A�ڒ��P�����ɂ��Q���̐����`�����̂̕\�ʂ���B��邩��A�p�^�[���`�̗��̂̕\�ʐς�144�|23�~�Q��98����2�ł��B�c�@�̕��@�Ɠ����ɂȂ���
�p�^�[���d�̗��̂Ȃ�A�����̂ǂ����̐ڒ��ӏ���44�����ŁA
�\�ʐς�144�|44�~�Q��56����2�ł��B
�ł͉��ɂU�̃p�^�[�����܂Ƃ߂��\�������Ă����܂��B�u���Ōv�Z���Ȃ����������ɂ��ẮA�݂Ȃ��e���ōl���Ă݂Ăق����Ǝv���܂��B(1)(2)(3)�̉͂��̃y�[�W�̈�ԉ��ɁA�A�`�G�ɂ��Ă̓e�X�g�҂̖��ɂ��܂��ˁB
�Ȃ��A�ڒ��ӏ��̋��ߕ��́A���̂悤�Ȏ���p�ӂ����̂Ŏg���Ă݂Ă��������B�ڒ��ʂ̖����͐ڒ��ӏ��̂���ɂQ�{�ł���B
�ڒ��ӏ��̐�
�����~���~(���|�P)�{���~(���|�P)�~���{(���|�P)�~���~��
| |
���� |
���� |
���� |
���{���{�� |
�ڒ��ʂ̖��� |
�\�ʐ� |
| A |
�P |
�P |
24 |
24 |
23����46�� |
96 |
| B |
�P |
�Q |
12 |
15 |
(1) |
�A |
| C |
�P |
�R |
�W |
12 |
(2) |
70 |
| D |
�P |
�S |
�U |
11 |
(3) |
�C |
| E |
�Q |
�Q |
�U |
10 |
44����88�� |
56 |
| F |
�Q |
�R |
�S |
�X |
�E�����G�� |
52 |
����͂⍡��͒����Ȃ�܂����ˁB���܂������H�{�N�������Ă��Ĕ��܂����B
����͂���ł����܂��ɂ��܂��傤�B�ł݂͂Ȃ���܂�����̍u���ŁI
�J�[�e���R�[��
���C�Â��ɂȂ����l�����邩�Ǝv���܂����A���������̂̊e�ӂ̒����������łȂ��Ă��悢�Ȃ��i����̖��͂P�ӂP�����̗����̂�ςݏグ�邩�琮������ł����c�j�R�ӂ��ׂĂ̒������u�R����24�ɂȂ鐔2.8845�c�v�̗����̂̏ꍇ�A�\�ʐς͖{���̍ŏ��ɂȂ�܂��B������2.8845�c��24�̗������i�R�捪�j������A�Z���ł͂�قǐ��l�Ɍb�܂�Ȃ�����v�Z���邱�Ƃ͂ł��܂���B�Z���ŏo�肳�����́A���̍u���̂悤�ɐ������肪�قƂ�ǂŁA�����̂ɂȂ�ׂ��߂��Ƃ��A���邢�͂R�ӂ̘a�������Ƃ��������Ȃ�Ƃ��ɕ\�ʐς��ŏ��ɂȂ�ƍl���Ă悢�ł��傤�B
�\�̉�(1)34����68���@(2)37����74���@(3)38����76��
�q���l�сr ���݁A�̎�t�ƃT�C�g��ł̐����Ҕ��\�͂��x�݂��Ă��܂��B���̍u�����Ńe�X�g�ƂȂ��Ă�����̓������o����A���̐��낪�C�ɂȂ���́A�g�b�v�y�[�W�̃��[���t�H�[������u�u���ԍ��v�Ɓu�v�������肭�������B����ɂ��Ă��Ԏ������Ă��������܂��B
|

 ����̍u���͗��̐}�`�ł��B�e�[�}�́A�����̂̑̐ς��Œ肵���Ƃ��A�\�ʐς��ǂ̂悤�ɕω����邩�̒����ł��B�̐ς������ł���������̋���͂����Ԃ�������ł���ˁB
����̍u���͗��̐}�`�ł��B�e�[�}�́A�����̂̑̐ς��Œ肵���Ƃ��A�\�ʐς��ǂ̂悤�ɕω����邩�̒����ł��B�̐ς������ł���������̋���͂����Ԃ�������ł���ˁB


