今回の第41講座は、「こんなに出される問題はめったにないよ」ぐらいよく出される問題で、２人が反対方向から２地点間を往復する旅人算の解説です。タイトルの意味は読んでいるうちにわかると思います。


どんどん書いてきたみんなの算数講座ですが、今回で早くも41講座目になるんですね。いったいこの講座はどこまで続くのでしょう？
じつはボクもこのホームページを立ち上げた頃、まさかこんなに続けて書くとは思っていませんでした。でもたくさんのみなさんのアクセスがうれしくてね。
もうここまできたんだから、どんどん増やしていくしかないね。ボクもがんばるので、みなさんも忘れずに読みにきてくださいね！

いきなり話がそれてしまいましたけど、ここから算数。

今回の旅人算は、上にも書いたけど、ホントによく出される問題です。
どこの塾でもやらないはずないから知っている人も多いと思うけど、知ってる人は復習になるし、知らない人はヤバい受験生にならないように、しっかり読んで理解してくださいね。

じゃあ問題です。

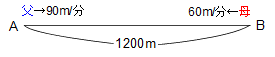Ａ、Ｂ２地点間の距離は1200ｍです。 お父さんはＡ地点を、お母さんはＢ地点を出発し、二人ともＡＢ間の往復を続けます。 お父さんの速さは分速90ｍ、お母さんの速さは分速60ｍです。 次の各問いに答えてください。ただし、場所についてはＡ、Ｂのうち近い方の地点と離れている距離で答えてください。 (1)お父さんとお母さんが１回目に出会うのは何分後ですか？ 　また、それはどこですか？ (2)お父さんとお母さんが２回目に出会うのは何分後ですか？ 　また、それはどこですか？ (3)お父さんとお母さんが５回目に出会うのは何分後ですか？ 　また、それはどこですか？

では(1)から。



１回目の出会いは簡単だと思います。

出会い算の基本公式　ウワサによると最近は出会い系公式というらしい…　
離れている距離　÷　速さの和　＝　出会うまでにかかる時間

を使って、1200÷（90＋60）＝８（分後）に出会うことがわかります。
出会う場所は、母の速さに８分をかけて、
Ｂ地点から480ｍ（←60×８）のところです。

(2)
さて２回目の出会い。



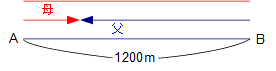
上の図をよく見てください。
２回目に出会う場合は、父の進んだ距離と母の進んだ距離の合計が、全体の1200ｍの３倍になっていることがわかります。

そう、２回目の場合はここがポイントなんです。

今回のような両方向からの往復問題では、
２回目に出会うまでに進む距離の合計は、全体の距離の２倍ではなく３倍になるのです。

３倍の距離があれば出会うまでの時間も３倍になるから、２回目に出会うのは１回目の８分後を３倍して24分後です。
出会う場所は母の速さに24分をかけて60×24＝1440ｍ。これは一度Ａ地点で折り返して1440−1200＝240ｍのところです。

え〜と、ちょっと無責任な先生になっちゃいますが、設問(3)はテスト編に回してみなさんにお考えいただくことにします。
(2)の２回目の出会いでわかったことから、想像力をかきたてれば、もう３回目でも４回目でもおわかりになるはずです。２回目の出会いがまだよくわかっていない人は、もう一度ゆっくり読んでみてくださいね。

じゃあ(3)も問題がテストですからね！
これで今回の第41講座を終わりにしたいとおもいま……

勇気ある生徒「ちょっと待ってよ、さんじゅつまんっ！」
さんじゅつまん「なに？私はこれからあっちで出前頼んでたおそばがきてるんで.....」
生徒「おそばより生徒の質問でしょ！３回目はどうなるの？」
さん「５倍じゃない？」
生徒「じゃ４回目は？」
さん「７倍じゃない？　もうおそばのびちゃうから行きますよ。」

２回目が３倍、３回目が５倍、４回目なら７倍。どうやらきれいな規則が見えてきたようです。テスト、がんばってくださいね。
第41講座、ホントにこれで終わります。

〈お詫び〉 現在、解答の受付とサイト上での正解者発表はお休みしています。答えを出され、その正誤が気になる方は、トップページのメールフォームから「講座番号」と「解答」をお送りください。正誤についてお返事させていただきます。