今回の第42講座では、前回に続いて速さのジャンルから運行間隔の問題を
解説しようと思います。コツさえつかめば簡単なのですが、最初はとっつきにくくて理解に苦しむ人が多いようです。ではさっそくお読みください。


運行間隔の問題とは、こういう問題です。↓

条件の数値が少なくてシンプルな問題でしょう？
でも確かに慣れていないと、どうやって手をつけたらよいか迷ってしまうかもしれませんね。

まず、状況を図に表してみましょう。



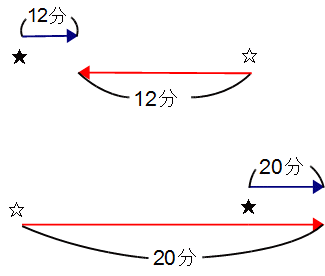
クルマが青い線、電車が赤い線です。

図（上）の説明
★の位置でクルマと「前の電車」が出会ったとして、（左に消えていく前の電車は書いてありません）
クルマが「次の電車」に出会うまでに12分かかることを表しています。
（☆印はクルマと「前の電車」が出会ったときの「次の電車」の位置です）

図（下）の説明
★の位置でクルマが「前の電車」に追い越されたとして、
クルマが「次の電車」に追い越されるまでに20分かかることを表しています。
（☆印はクルマが「前の電車」に追い越されたときの「次の電車」の位置です）

さて、上の２つの図を同時によく見ると、
青い線の合計と赤い線の差が等しくなっていることがわかります。

青い線の合計　⇒　クルマが12＋20＝32分で進む距離
赤い線の差　　⇒　電車が20−12＝８分で進む距離

つまり、クルマが32分で進む距離と電車が８分で進む距離が等しいのです。

ここで速さの基礎知識
距離が同じなら　所要時間の比と速さの比は逆になる　を用いて、

所要時間　クルマ：電車＝32：８＝４：１より、
速さ　　　クルマ：電車＝１：４
これで(1)の答えを求めることができました。

(2)で求めるのは電車の運行間隔です。
電車の運行間隔とは、電車と電車の間隔が何分あいているか、
つまり、電車と電車の間隔を電車が何分で進むかということです。

電車と電車の間隔は、さきほどの図に示した〈★と☆の距離〉のことです。
上下どちらの図で考えても大丈夫ですが、たとえば上の図で考えるなら、クルマが12分で進む距離を電車は３分（←等しい距離の所要時間は1/4）で進むから、〈★と☆の距離〉を電車が進む時間は12＋３＝15分。
これが(2)の解答です。(1)が出てしまえば(2)は簡単ですね。
※下の図で考えても同じことです。 クルマが20分で進む距離を電車は５分（20÷４）で進むから、〈★と☆の距離〉を電車が進む時間は20−５でやはり15分です。

＊＊＊
運行間隔の問題、理解していただけたでしょうか。
問題に出てくる数値が少ないから、大げさな計算が始まるはずはないのですが、初めての人たちに理屈の説明も一緒にやると、けっこう面倒な問題なんですよね。どこの塾でも、塾の先生泣かせの問題かもしれません。
もしよかったら、最後に〈おみやげ公式〉を残しておきますから、受験が近い人などは頭に入れておくと便利だと思います。

ジャーン！　運行間隔問題の＜おみやげ公式＞
（追い越される時間−出会う時間）：（追い越される時間＋出会う時間）
　＝クルマの速さ：電車の速さ　

今回の問題なら（20−12）：（20＋12）＝８：32＝１：４
速さの比を求めるなら、この式一発でハイ終わりですね！
あ、片方はだいたい電車だけど、もう片方（遅いほう）はクルマとは限らないですよ。そこまで心配するのはボクの仕事じゃないでしょうね。クルマのかわりがバスでもオートバイでも自転車でももちろん同じです。

ではでは今回はこんなところで。
また次回の講座で元気に算数を勉強しましょう！　さようなら。