今回はホントにホント。教え子たちのセリフに刺激されて書いた講座です。内容は、有名な算数の先生が発案された時計算の解法なのですが、なるほどなかなか素晴らしい解法であります。


教え子のナマスケ
「先生のホームページってシャドーの説明がないよね。先生知らないんでしょ？」
困った顔の私を見てすかさずもう一人。
教え子のマセオ
「なんだ先生、知らないのかぁ。算数の先生がシャドー知らなきゃダメじゃん？」

まったく小学生という人種は言葉を選びません。ボキャブラリーが少ないということもあるでしょうが、表現が剛速球のストレート！まあ、彼らに悪意はないんですけどね。これは大勢の小学生たちと接して、身をもって感じてきたことでありますが、
でも　言いたいことを隠して黙っている大人よりは、ずっと好きです。

シャドー。
これは「中学への算数」という東京出版発行の雑誌から生まれた算数用語。時計算の解法テクニックの名称で、同誌中心ライター、栗田先生のご発案だったと思います。
もちろんだいぶ前から何度も読んで知っていました。ですが、ご発案者がハッキリしていましたし、この講座では今まで掲載を遠慮してました。

…という、取り上げなかった理由がきちんとあるわけですが、ナマスケたちのセリフを黙認するのも悔しいから、今回の講座で１問だけ紹介してみようと思います。
※「中学への算数」は、塾の算数教師のバイブルと呼ばれるほど、充実した内容の素晴らしい雑誌です。まだ読んだことのない生徒さんやご父兄は、ぜひ一度お読みになることをお勧めします。

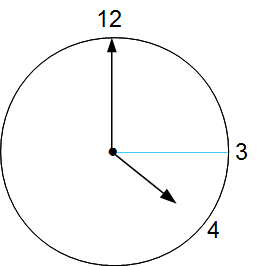
上の図は４時ジャストの時計のようすです。
ここから何分か経過したときに、長針と短針のちょうどまん中にブルーで示した「３」のラインが入るということです。
必ずしもシャドーを使わなくても解くことはできますが、確かにシャドーを使うと、とても速く解けるのは間違いないです。
その考え方は……。

　

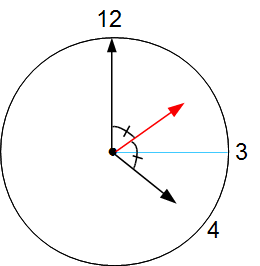
つねに長針と短針の中央を動く架空の針（シャドー針・赤色）を想定します。そしてそのシャドー針が「３」を示すラインに重なるときが解答になると考えるのです。

時計の長針は分速６°　短針は分速0.5°だから、シャドー針はそれらの平均的なスピード
つまり（６＋0.5）÷２＝分速3.25°です。

シャドー針と「３」ラインの４時ジャストでの隔（へだ）たりは30°
（理由→４時ジャストは長針と短針の角度が120°だから 90−120÷２＝30°）

したがって、シャドー針が「３」ラインに重なるまでの時間は、
30°÷3.25°＝30÷13/4＝120/13＝9と3/13（分）

求める時刻は４時9と3/13分です。

＊＊＊
以上教え子に誘発されてシャドー針の解説でした。
便利だなぁと思った人は、使えるときにどんどん使ってくださいね。
え？　シャドーの意味？
英語でshadowは陰（かげ）という意味なので、〈忍者のように姿が見えない架空の針〉という意味だと思います。たしかそんな感じの説明を読んだ覚えがありますね。

では今回の講座はこれで終わります。
テストの問題はシャドーも使えますが、別にこだわる必要はありません。他の解き方をしてくれてもかまいませんよ。
それではまた次回の講座でお会いいたしましょう！

Special Thanks! 中学への算数　東京出版のホームページはこちら