この第56講座の改訂版を姉妹サイト中学受験の算数知恵宝庫(スマホ対応)にNewみんなの算数講座56としてアップしています。 ★講座タイトルを「何個壊れて何個無事？」に変更しました これまで以上に読みやすい文体、装飾、見やすい図形を心がけました。算数知恵宝庫にもぜひいらしてくださいね。

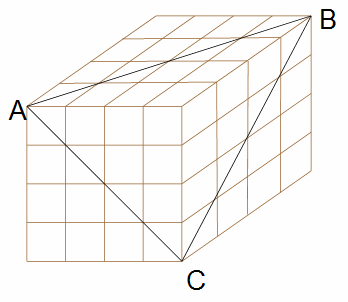
今回の講座は、立方体を積み上げるところまでは第15講座と似ています。 第15講座では色塗りでしたが、今回は包丁（ほうちょう）で切って、壊れたのか無事なのかを考えます。面白い問題ですよ。 では少しだけ得意の前置きから…。 図形の講座を書くときは、一つのソフトではできません。文字を入力するソフトとは別に図形作成ソフトも使います。最初はなかなか慣れませんでしたから、昔書いた講座などを見ると、かなりヘタだったなぁ〜と自分で思います。まぁそれも思い出？ いまでもプロの人に比べたら全然ダメでしょうけど、昔に比べたらだいぶうまく書けるようになってきました。ときにはちょっと失敗の図になっちゃうかもしれませんが、シロートなりに なるべく見やすく作っていきたいと思います。まだまだうまくなれるかな??? さて今回の問題です。 左図のように64個（４×４×４）の小立方体を積み上げて作った大きな立方体があります。 この大きな立方体を３点ＡＢＣを通る 平面で切断します。 （切り口は正三角形） このとき、64個の小立方体のうち、 壊れるもの（負傷者）と 無傷なもの（生存者）は それぞれ何個ですか？ みなさんならこの問題、どう考えますか？ なんとなく見た目で判断しようととすると、けっこう頭がこんがらがります。ハッキリと負傷、生存が確認できるものもあるけど、こいつはどっちだろう？って悩んでしまう微妙なものもいくつかあります。かなり空間センスのある人でも、見た目で答えを出すのは大変でしょう。 オススメはこんな考え方。 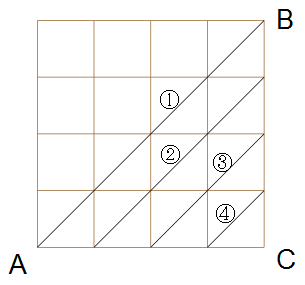←このように、真上から見た平面図を書き、切断面の移動を斜め線で記入します。 ※よほど複雑な問題でなければ１枚の平面で足りるでしょう。 切断面は一番上の段を斜め線�@から切り始め、斜め線�Aまで進んだときに一番上の段を切り終えます。 したがって、一番上の段の負傷者は斜め線�@と�Aの間にある７個です。 切断面は上から二段目を斜め線�Aから切り始め、斜め線�Bまで進んだときに、上から二段目を切り終えます。上から二段目の負傷者は、斜め線�Aと�Bの間にある５個です。 このあとも同じです。 切断面は上から三段目を斜め線�Bから切り始め、斜め線�Cまで進んだときに、上から三段目を切り終えます。上から三段目の負傷者は、斜め線�Bと�Cの間にある３個です。 一番下の段は、切断面が斜め線�Cから切り始め、最後は頂点Ｃに抜けていきます。一番下の段の負傷者は、斜め線�Cより下にある１個です。 以上のことから、負傷する小立方体は全部で ７＋５＋３＋１＝16個 全体の個数から引き算して、生存している小立方体は 64−16＝48個　となります。 切断面を斜め線で追いかける考え方　楽しいでしょう？ もっとも上の問題は、全体が４×４×４の立方体になっていて、切断面が中途半端な場所を通らないから、空間センスのある人や勘（かん）のいぃ人なら、見た目だけでわかっても不思議ないかもしれません。 でも全体の形が変わってくると、見た目での判断はもっと難しくなりますよ。 たとえばこんなの↓ さきほどと同じようにＡＢＣを通る平面で切断したとき、負傷者と生存者の個数をそれぞれ求めてください。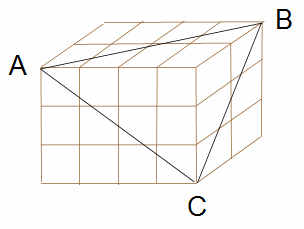 今度は最初の問題と違い、全体が立方体ではないため、切断面が、小立方体の頂点ではない中途半端な箇所を通ります。全体の個数は２×４×３＝24個でさっきより少ないですが、見た目での判断はこちらの方が難しいでしょう。 やはりさきほど解説した、上から見た平面を書いて切断面を追いかける方法がよいですね。 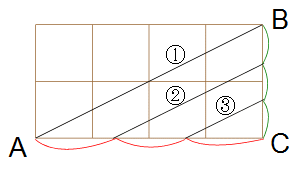赤と緑の印は、ＡＢ、ＢＣをそれぞれ３等分している意味です。 切断面は、一番上の段を斜め線�@から切り始め、斜め線�Aまで進んだときに一番上の段を切り終えます。一番上の段の負傷者は斜め線�@と�Aの間にある６個です。 切断面は、上から二段目を斜め線�Aから切り始め、斜め線�Bまで進んだときに上から二段目を切り終えます。上から二段目の負傷者は、斜め線�Aと�Bの間にある４個です。 切断面は、一番下の段を斜め線�Bから切り始め、最後は頂点Ｃに抜けます。一番下の段の負傷者は、斜め線�Bより下にある２個です。 以上のことから、負傷する小立方体は全部で ６＋４＋２＝12個 全体の個数から引き算して、生存している小立方体も 24−12＝12個　です。 以上立体切断戦争における負傷者と生存者数のレポートでした（笑） どうでしたか？　よくわかったって？　それはきっとボクの説明がうま…　　じゃなくて、みなさんが算数に強くなっている証拠でしょうね。もう56個目の講座ですもん。 小学生の算数でも、中高生の数学でも、生徒の理解がもっとも悪いのはなんといっても空間図形の問題です。立体という高さを持ったものを、無理して平面に収めて考えてますから、難しいのは当たり前かもしれませんね。 しかし入学試験では限られたパターンの問題しか出ませんから、ひととおりのパターンを勉強しておけば、そんなに困ることはないと思います。 ＊＊＊ たくさんの講座を書いています。算数、大好きになってくださいね。 いまの生徒さんには夢がある.....将来、総理大臣目指したって、宇宙飛行士目指したって、アナウンサー目指したって、何を目指したって自由だよね。夢が持てていいなぁ..... ボクがいまそんなことを口に出したら、大丈夫???熱でもある???体温計持ってこようか???ってなっちゃいますでしょ？ あ〜あ〜、こうしていつも脱線していくさんじゅつまんの授業。でも間違いなく確かな算数を楽しく伝えております。算数の力がみなさんの将来の夢を叶えるお手伝いをしますように!!! ではまた次回、なるべく近いうちに！

東京および近県で中学受験を目指すお子様への算数家庭教師はお任せください。 下記リンク「中学受験算数家庭教師について」をお読みになり、 ページ内の連絡フォームよりご連絡ください。お問い合わせも歓迎です。 東京の中学受験 算数家庭教師さんじゅつまん｜ 中学受験算数家庭教師について｜ プロフィール｜著書目録｜みんなの算数講座目次｜みんなの算数講座カラーファイル｜ また来てね問題集｜算数界の専門用語｜数の雑学｜ 一般のご連絡フォーム｜家庭教師用ご連絡フォーム｜