今回はちょっと難解な速さの問題を題材にします。経験がなくて初見で解くのはかなり厳（きび）しいと思います。ボクも若い頃、解けませんでした。ぜひ一度読んでおいてください。


算数の問題の出題者は、難しい問題をこしらえるために、ときどき現実的ではない設定を用意します。今回の問題もその一つですね。

数人のグループがＡ地点からＢ地点に向かいますが、クルマが一台しかなく乗りきれない...
そこでグループは二手（ふたて）に分かれ、片方のグループはクルマで目的地に向かい、もう片方のグループは歩いて目的地に向かいます。
すると当然クルマ組の方が速いですから、ドライバーは途中で同乗者を下ろし徒歩組を迎えにいきます。冷たい...普通最後まで送るよね〜
そしてどこかで徒歩組を見つけると、彼らを乗せてクルマは再度目的地へと向かいます。
結果として２つのグループは同時に目的地へ到着！　

問題文を書いていて疲れました。みなさんも読んでいて疲れたかも知れませんね。おわびに状況を図でも示しておきます。

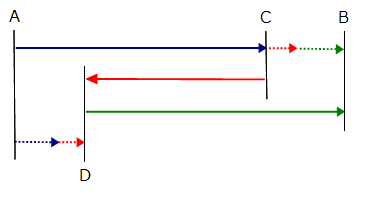
←こういう状況です。
実線がクルマで点線が歩きです。
色で分けたのは時間の流れです。
同じ色のところが同じ時間ですね。
でもこの問題、こういう直線図だけでは
状況が見えにくいかもしれません。


じつはこの問題、平行四辺形グラフの問題と呼ばれていて、横軸を時間、タテ軸を距離にしたグラフを書くと、その状況が美しい平行四辺形のグラフになります。
↓こんな感じです。


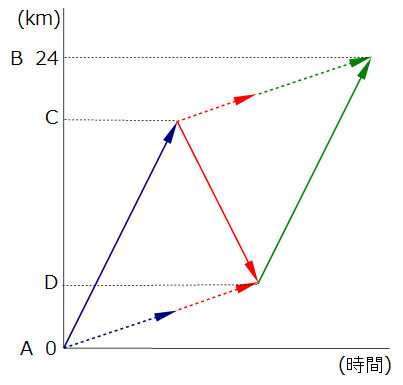
最初の図と同じように、クルマの進行を実線、歩く子どもたちを点線にしました。
時間の流れを色で区別しています。
青　クルマがＣ地点で子どもを降ろすまで
赤　引き返したクルマが子どもを拾うまで
緑　Ｂ地点に到着するまで
です。

なぜこのような平行四辺形のグラフになるかといえば、全員が同時にＢ地点に到着したということは子どもたち２グループがクルマに乗っていた時間と歩いていた時間が同じになるからです。

もし、クルマに乗っていた時間と歩いた時間が違えば、２グループが同時にＢ地点に到着することはありません。長い時間クルマに乗っていたグループが先にＢ地点に到着するでしょう。
つまり、どちらのグループも同じだけクルマに乗って、同じだけ歩いたのです。そのことから上のような美しい平行四辺形グラフができあがります。

さて、ここで速さの基礎知識を使います。

所要時間が等しいとき、(進んだ距離の比)＝(速さの比)になるから、
〈歩きの速さ〉：〈クルマの速さ〉＝４：36＝１：９より、
〔ＡＤ間の距離〕を１とすると、
〔ＡＣ間の距離＋ＣＤ間の距離〕が９になります。
※子どもたちがＡＤ間を歩いているとき、クルマはＡからＣまで行き、さらにＣからＤへ戻っています。

比を記入したグラフをもう一度のせますね。見にくいとまずいからグラフのカラーは消しました。


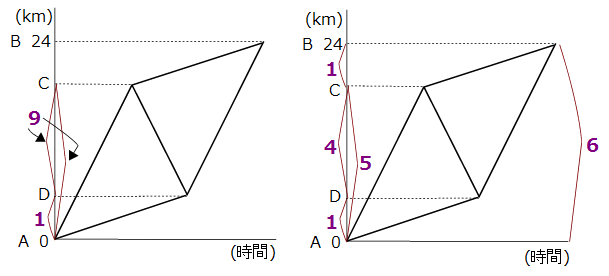
ではこのグラフを使いながら、さらに解説を進めます。

ＣＤ間の距離は （９−１）÷２＝４
ＡＢ間の距離は、１＋４＋１＝６
また、クルマが走った距離の合計は ９＋４＋１＝14 です。
※ＢＣ間の距離はＡＤ間と同じです。２グループが歩いた時間が同じだからです。

(1)
ＣＤ間の距離は、ＡＢ間の距離に対して６のうちの４ つまり2/3です。
ＡＢ間の距離は24ｋｍだからＣＤ間の距離は 24×2/3＝16ｋｍです。…(1)の答え

(2)
出発してから到着するまでにかかる時間は、クルマが走った距離の合計をクルマの速さで
わります。
クルマが走った距離の合計はＡＢ間の距離の14/6 　つまり7/3倍だから、
24×7/3＝56ｋｍ　←クルマが走った距離の合計
クルマの速さは時速36ｋｍだから、出発してから到着するまでにかかる時間は
56÷36＝56/36(時間)＝14/9(時間)＝１と5/9（時間）…(2)の答え

＊＊＊
どうでしたか？　理解できたかなあ？
今回どうしてもこの問題を解説したくて、張り切って図を作ってやってみましたが、少し難しかったかもしれませんね。まだ不安な人はこのページをカラー印刷して、何度か読むようにしてくださいね。わかったときの爽快感（そうかいかん）最高だと思いますよ。

では今回はここまでにします。次回の講座に乞（こ）うご期待！です。