 夁嫀栤PART1 |
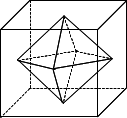 搤帄 搤帄塃恾偺傛偆偵丄侾曈偺挿偝偑係cm偺棫曽懱偺奺柺偺懳妏慄偺岎揰傪偲傝丄偦傟傜傪捀揰偲偡傞棫懱(惓敧柺懱)傪嶌傝傑偡丅偙偺棫懱偺懱愊傪媮傔偰偔偩偝偄丅 戝愥 9傪楢懕偡傞惍悢偺榓(惍悢偺屄悢偼2屄埲忋側傜帺桼)偱昞偡曽朄偼[4+5]偲[2+3+4]偺2捠傝偑偁傝傑偡丅偱偼81傪楢懕偡傞惍悢偺榓偱昞偡曽朄偼壗捠傝偁傝傑偡偐丠忋偺傛偆偵幃偲偲傕偵摎偊偰偔偩偝偄丅 彫愥 師偺傛偆偵俀働僞偺摨偠悢偳偆偟傪偐偗偰丄偱偒偨係働僞偺悢偺拞墰偺俀働僞傪庢傝弌偟偰怴偟偄悢偲偡傞偙偲傪孞傝曉偟傑偡丅 偨偲偊偽嵟弶偺悢偑65偺偲偒丄 65亊65亖4225 佀2斣栚偺悢偼22 22亊22亖484 佀偙傟偼0484偲峫偊偰3斣栚偺悢偼48 48亊48亖2304 佀4斣栚偺悢偼30 嵟弶偺悢(1斣栚偺悢)偑79偺偲偒丄999斣栚偺悢傪媮傔偰偔偩偝偄丅 棫搤 係偮偺惍悢俙,俛,俠,俢偑偁傝傑偡丅偙傟傜偼師偺俆偮偺忦審傪偡傋偰枮偨偟偰偄傑偡丅 嘆俙偼侾埲忋丂嘇俢偼俁埲壓丂嘊俙偼俛埲壓丂嘋俛偼俠埲壓丂嘍俠偼俢埲壓 俙,俛,俠,俢偺慻崌偣偼慡晹偱壗捠傝峫偊傜傟傑偡偐丠偑 憵崀 働乕僉偑擖偭偨敔偑17敔偁傝傑偡丅敔偺戝偒偝偵傛偭偰俁屄擖傝丄俆屄擖傝丄俈屄擖傝偺俁庬椶偑偁傝丄働乕僉偼慡晹偱73屄偁傝傑偡丅偁傞儗僗僩儔儞偺拲暥偱働乕僉偑65屄昁梫偵側偭偨偺偱丄俁屄擖傝偺敔傪偡傋偰俀屄擖傝偵偟偨偲偙傠丄偪傚偆偳65屄偵偡傞偙偲偑偱偒傑偟偨丅敔偼偦傟偧傟壗敔偢偮偁傝傑偟偨偐丠 姦業 戝恖係恖偱傗傞偲10擔偐偐傞巇帠傪丄戝恖2恖偲巕嫙係恖偱傗傞偲16擔偐偐傝傑偡丅偙偺巇帠傪戝恖俋恖偲巕嫙俉恖偱傗傞偲壗擔偐偐傝傑偡偐丠 廐暘 偁傞妛峑偱懖嬈暥廤傪嶌傞偙偲偵側傝丄報嶞壆偝傫偵憡択偟傑偟偨丅偼偠傔偺50嶜偼1嶜偵偮偒200墌丄51嶜栚偐傜80嶜栚傑偱偼1嶜偵偮偒180墌丄81嶜栚偐傜120嶜栚傑偱偼1嶜偵偮偒150墌丄121嶜栚偐傜偼1嶜偵偮偒110墌偱偱偒傞偲尵傢傟傑偟偨丅慡晹偱壗嶜棅傫偩偲偒丄1嶜偵偮偒偪傚偆偳150墌偵側傝傑偡偐丠 敀業 暘曣偑2014偱偁傞2013屄偺恀暘悢(暘巕偑暘曣傛傝彫偝偄暘悢)偑偁傝傑偡丅 1/2014丂2/2014丂3/2014丂乧乧乧丂2012/2014丂2013/2014 偙偺側偐偱栺暘偡傞偙偲偑偱偒傞暘悢偼慡晹偱壗屄偁傝傑偡偐丠 亂僸儞僩亃2014傪慺場悢暘夝偡傞偲2亊19亊53偱偡丅 張弸 俆屄偺儅儞僑乕偲俈屄偺僷僷僀儎偑偁傝傑偡丅偙傟傜12屄偺壥暔傪俙,B,C,D偺4恖偵3屄偢偮暘偗傞曽朄偼慡晹偱壗捠傝偁傝傑偡偐丠 棫廐 偁傞巇帠傪俙偝傫侾恖偱傗傞偲12帪娫偐偐傝丄俙偝傫偲俛偝傫偺俀恖偱傗傞偲係帪娫偐偐傝丄俛偝傫偲俠偝傫偺俀恖偱傗傞偲俀帪娫偐偐傝傑偡丅嵟弶俛偝傫偑偙偺巇帠偺係暘偺侾傪侾恖偱巇忋偘丄巆傝偺巇帠傪俙偝傫偲俠偝傫偺俀恖偱巇忋偘傑偟偨丅嵟弶偐傜偐偐偭偨帪娫偼壗帪娫壗暘偱偡偐丠 戝弸 暘悢傪仏/仏(暘巕/暘曣)偺傛偆偵昞婰偟傑偡丅巻偵彂偄偰偍峫偊偔偩偝偄丅 1傛傝彫偝偄暘悢偑壓偺傛偆偵偁傞婯懃偵偟偨偑偭偰暲傫偱偄傑偡丅100斣栚偺暘悢傪媮傔偰偔偩偝偄丅 1/3丂2/3丂1/9丂2/9丂4/9丂5/9丂7/9丂8/9丂1/27丂2/27丂4/27丂5/27乧乧乧 彫弸 俙,俛,俠,俢,俤偺俆恖偑俆媟偺堉巕偵墶堦楍偱嵗偭偰偄傑偡丅偙傟偐傜嵗傝曽傪曄偊傛偆偲偟偰偄傑偡偑丄俆恖慡堳偑崱偲偼堘偆堉巕偵嵗傞嵗傝曽偼壗捠傝偁傝傑偡偐丠 壞帄 暘悢傪乽乧暘偺乧乿偺傛偆偵彂偒傑偡偺偱丄巻偵彂偄偰偍峫偊壓偝偄丅 乽仩暘偺俆乿偲乽俆暘偺仩乿傪偨偡偲乽俁暘偺仮乿偵側傝傑偡丅仩偲仮偼偲傕偵惍悢偱偡偑丄仮偼俁偺攞悢偱偼偁傝傑偣傫丅仮偵偁偰偼傑傞嵟傕彫偝偄惍悢傪媮傔偰偔偩偝偄丅 (拲)俀儢強偺仩偵偼摨偠惍悢偑擖傝傑偡丅 鋳庬 敔偺拞偵敀嬍偲愒嬍偑2:1偺妱崌偱擖偭偰偄傑偡丅峀応偵偄傞巕嫙偨偪偵敀嬍傪7屄偢偮丄愒嬍傪2屄偢偮攝傞偲丄敀嬍偼偪傚偆偳側偔側傝丄愒嬍偼12屄梋傝傑偟偨丅峀応偵偄傞巕嫙偨偪偼壗恖偱偡偐丠 彫枮 梕婍俙偵偼400g丄梕婍俛偵偼600g偺擹偝偺偪偑偆怘墫悈偑偦傟偧傟擖偭偰偄傑偡丅偄傑梕婍俙偺怘墫悈偺敿暘偺検傪梕婍俛偵擖傟偰崿偤崌傢偣丄師偵梕婍俛偺怘墫悈偺敿暘偺検傪梕婍俙偵擖傟崿偤崌傢偣傑偟偨丅寢壥丄梕婍俙偺怘墫悈偺擹搙偑9亾丄梕婍俛偺怘墫悈偺擹搙偑10亾偵側傝傑偟偨丅嵟弶偺怘墫悈俙丄俛偺擹搙偼偦傟偧傟壗亾偱偟偨偐丠 棫壞 偁傞價儖偺僄儗儀乕僞乕偼1奒暘忋偑傞偺偵6昩丄奺奒偵掆巭偟偨偲偒偼12昩巭傑傝傑偡丅搑拞偺奒偱壓偑傞偙偲偼側偔丄奐暵偺墑挿傗抁弅傕偱偒傑偣傫丅 (1)丂6奒偱偲傃傜偑暵傑偭偰偐傜11奒偱偲傃傜偑暵傑傞傑偱偺僄儗儀乕僞乕偺忋偑傝曽偼慡晹偱壗捠傝偱偡偐丠 (2)丂(1)偺偦傟偧傟偵偐偐傞帪娫偺憤榓偼壗暘壗昩偱偡偐丠 崚塉 偁傞彫妛峑偺堏摦嫵幒偱偼丄妱傝摉偰傜傟偨晹壆悢偑寛傔傜傟偰偄傑偟偨丅偦偺晹壆悢偼6恖晹壆丄7恖晹壆丄8恖晹壆偑偁傢偣偰17幒偁傝傑偡丅偙傟傜偺晹壆傪慡晹巊梡偡傞偲120恖廂梕偱偒傑偡丅偲偙傠偑妛峑偺惗搆悢偑130恖偺偨傔丄6恖晹壆傪7恖丄7恖晹壆傪8恖偲偟偨傜丄偪傚偆偳慡堳廂梕偡傞偙偲偑偱偒傑偟偨丅6恖晹壆丄7恖晹壆丄8恖晹壆偺晹壆悢傪偦傟偧傟媮傔偰偔偩偝偄丅 惔柧 2014擭偺4寧5擔偼搚梛擔偱偟偨丅2014擭偺師偵4寧5擔偑搚梛擔偵側傞偺偼惣楋壗擭偱偡偐丠 弔暘 3働僞偺惍悢偺奺埵偺悢帤偺榓傪寁嶼偟傑偡丅偨偲偊偽3働僞偺惍悢偑134側傜1+3+4亖8偲偄偆梫椞偱偡丅偙偺榓偑24傛傝彫偝偔側傞3働僞偺惍悢偼慡晹偱壗屄偁傝傑偡偐丠 孾瀛 1偐傜1000傑偱偺惍悢偺偆偪丄566傗646偺傛偆偵丄6偲偄偆悢帤偑2屄偱偰偔傞惍悢傪偡傋偰壛偊傞偲偄偔偮偵側傝傑偡偐丠 塉悈 壓偐傜忋傑偱7抜偺奒抜偑偁傝傑偡丅偙偺奒抜傪壓偐傜忋傑偱偺傏傞偲偒偵丄1曕偱偺傏傟傞抜悢偼1抜丄2抜丄3抜偺偄偢傟偐偱偁傞傕偺偲偟傑偡丅偙偺奒抜偺偺傏傝曽偼慡晹偱壗捠傝偁傝傑偡偐丠丂偨偲偊偽偡傋偰1抜偢偮偺傏傞乹1抜-1抜-1抜-1抜-1抜-1抜-1抜乺偺傛偆側偺傏傝曽偑1捠傝偺偺傏傝曽偱偡丅 棫弔 偁傞3働僞偺惍悢俙偑偁傝傑偡丅俙偵12傪壛偊傞偲13偱妱傝愗傟丄俙偵18傪壛偊傞偲19偱妱傝愗傟傑偡丅傑偨丄俙偺昐偺埵偲堦偺埵偺悢帤傪擖傟偐偊傞偲丄俙傛傝彫偝偔側傝傑偡丅惍悢俙傪媮傔偰偔偩偝偄丅 戝姦 1墌嬍2枃丄5墌嬍2枃丄10墌嬍3枃丄50墌嬍1枃偑偁傝傑偡丅偙偺峝壿傪1枃埲忋巊偭偰偪傚偆偳暐偊傞嬥妟偼壗捠傝偁傝傑偡偐丠 彫姦 係偮偺堎側傞惍悢偑偁傝丄偙偺偆偪侾偮偩偗偑嬼悢偱偡丅係偮偺惍悢偺拞偐傜堎側傞俀偮偺惍悢傪慖傫偱榓傪媮傔傞偲21,24,26,27,29,32偵側傝傑偡丅偼偠傔偺係偮偺惍悢傪媮傔偰偔偩偝偄丅 搤帄 偁傞巇帠傪A丄B偺俀恖偑椡傪崌傢偣偰偡傞偲丄A偼侾恖偱偡傞偲偒傛傝傕侾妱懡偔偺巇帠偑偱偒丄B偼侾恖偱偡傞偲偒傛傝傕俀妱懡偔偺巇帠偑偱偒傑偡丅偙偺巇帠傪A丄B俀恖偱俇帪娫摥偄偰慡懱偺2/5(5暘偺2)傪巇忋偘丄梻擔偼B偑侾恖偱俇帪娫摥偒傑偟偨丅偦傟偱傕傑偩慡懱偺13/30(30暘偺13)偑巆偭偰偄傑偡丅A1恖偱偙偺巇帠傪偡傞偲壗帪娫偐偐傝傑偡偐丠 戝愥 悈杕偝傫偼搆曕偱A抧揰偐傜B抧揰傑偱傪墲暅偟傑偟偨丅峴偒偼40暘偛偲偵5暘偺媥偗偄傪偟丄3帪娫26暘偱B抧揰偵拝偒傑偟偨丅婣傝偼2攞偺懍偝偱曕偒丄30暘偛偲偵5暘偺媥偗偄傪偟側偑傜A抧揰偵婣傝傑偟偨丅婣傝偼壗帪娫壗暘偐偐傝傑偟偨偐丠 彫愥 偁傞彫悢傪暿偺彫悢偱傢傝傑偡丅彜傪侾偺埵傑偱媮傔傞偲偁傑傝偼3.6偱偡丅傢傝偒傟傞傑偱寁嶼偡傞偲彜偼12.8偱偡丅偙偺傢傝嶼偺幃傪峫偊偰偔偩偝偄丅 搤帄 搤帄 忋壓俀屄偺惓巐妏偡偄偵暘偗偰懆偊丄偦傟傜偺崌寁偲偟偰懱愊傪寁嶼偟傑偡丅仏忋壓偺惓巐妏偡偄偼崌摨側棫懱偱偡 忋壓偵暘偗偨偲偒偺嫬奅偵偁偨傞惓曽宍傪掙柺偲峫偊傑偡丅偙偺惓曽宍偺柺愊偼棫曽懱偺昞柺偵偁傞惓曽宍偺柺愊偺敿暘偱偡丅仏棫曽懱偺昞柺偺惓曽宍偺奺曈偺拞揰傪偮側偄偩宍 傑偨丄忋壓偺惓巐妏偡偄偺崅偝偼偦傟偧傟俀cm偱偡偑丄俀屄崌傢偣偰係cm偲峫偊偰偐傑偄傑偣傫丅偡偄偺懱愊偩偐傜嵟屻偵1/3傪偐偗傞偙偲傪朰傟側偄偱偔偩偝偄丅 (係亊係亊1/2)亊係亊1/3亖32/3亖10偲2/3們倣3 戝愥 戝愥 埲慜乽傒傫側偺嶼悢島嵗乿偱庢傝忋偘偨偙偲偑偁傞栤戣偱偟偨丅 堦斒偵丄偁傞惍悢傪楢懕偡傞惍悢偺榓偱昞偡偙偲偑偱偒傞僷僞乕儞悢偼丄偦偺惍悢偑帩偮1埲奜偺婏悢偺栺悢偺屄悢偲摍偟偔側傝傑偡丅 81偺栺悢偼1,3,9,27,81偺俆屄偱偡偑丄偙偺偆偪1傪彍奜偟偨係捠傝偑夝摎偵側傝傑偡丅 嬶懱揑偵偼忋偺夝摎偵帵偟偨傛偆偵側傝傑偡丅偔傢偟偄峫偊曽偵偮偄偰偼戞55島嵗傪偍撉傒偵側偭偰偔偩偝偄丅 彫愥 彫愥 堈偟偄廃婜嶼偺栤戣偱偟偨丅 尰傟傞悢偺斣崋偲偟偰儅儖埻傒悢帤傪梡偄傑偡丅 嘆79 嘇79亊79亖6241仺24 嘊24亊24亖0576仺57 嘋57亊57亖3249仺24 埲壓丄嬼悢斣栚偼24丄婏悢斣栚偼57傪孞傝曉偡偙偲偵側傝丄999(婏悢)斣栚偺悢偼57偱偡丅 棫搤夝摎丂15捠傝 棫搤夝愢 偙偺栤戣偺戣堄偼師偺傛偆偵懆偊傞偙偲偑偱偒傑偡丅 乽1,2,3偺悢帤傪巊偄丄塃懁偺悢帤偑嵍懁偺悢帤傛傝彫偝偔側傜側偄傛偆偵係働僞偺惍悢ABCD傪嶌傞丅乿 偙偺忦審傪枮偨偡係働僞偺惍悢ABCD傪彫偝偄弴偵峫偊偰偄偒傑偡丅 A=1偺偲偒丄 1111丂1112丂1113丂1122丂1123丂1133 1222丂1223丂1233丂1333丂(10捠傝) A=2偺偲偒丄 2222丂2223丂2233丂2333丂(4捠傝) A=3偺偲偒丄 3333丂(1捠傝) 偙傟傜傪崌寁偟偰丄媮傔傞夝摎偼15捠傝偱偡丅 憵崀夝摎丂俁屄擖傝乧俉敔丄俆屄擖傝乧俈敔丄俈屄擖傝乧俀敔 憵崀夝摎 俁屄擖傝偺敔傪俀屄擖傝偵曄偊偨偙偲偱廂傑偭偨働乕僉偺憤悢偑8屄(亖73亅65)尭偭偰偄傞偐傜丄俁屄擖傝偺敔偑俉敔偩偭偨偙偲偑傢偐傝傑偡丅 偡傞偲俆屄擖傝偲俈屄擖傝偺敔偺崌寁偑俋敔(亖17亅俉)丄廂傑偭偰偄傞働乕僉偺悢偑49屄(亖73亅俁亊俉)偲傢偐傝傑偡丅 巼怓偱帵偟偨忦審傪巊偭偰偮傞偐傔嶼傪夝偔偲丄俆屄擖傝偺敔偑俈敔丄俈屄擖傝偺敔偑俀敔偲媮傔傞偙偲偑偱偒傑偡丅 仏偮傞偐傔嶼偵偮偄偰偼偙偪傜偺暅廗婰帠傪偳偆偧両 姦業夝摎丂4擔 姦業夝愢 戝恖侾恖偑侾擔偐偐傞巇帠検傪侾偲偡傞偲丄戝恖係恖偑10擔偐偐傞巇帠検偼係亊10亖40偱偡丅 偙傟偲摨偠巇帠傪戝恖俀恖偲巕嫙係恖偱16擔偐偐傞偐傜丄戝恖俀恖偺16擔暘(俀亊16亖32)傪嵎偟堷偔偲丄巆傝偺巇帠偼俉(亖40亅32)偲側傝丄偙傟偼巕嫙係恖偑16擔偐偐偭偨巇帠検偱偡丅 偟偨偑偭偰巕嫙侾恖偺侾擔暘偺巇帠検偼俉亐(係亊16)亖8/64亖1/8偱偡丅 戝恖俋恖偲巕嫙俉恖偑侾擔偱偡傞巇帠検偼侾亊俋亄1/8亊俉亖俋亄侾亖10偩偐傜丄40偺巇帠傪廔偊傞偵偼40亐10亖係擔偐偐傞偙偲偵側傝傑偡丅 廐暘夝摎丂205嶜 廐暘夝愢丂 嶜悢偑傢偐偭偰偄傞120嶜傑偱偺晹暘偱丄1嶜偁偨傝偺暯嬒偺抣抜傪寁嶼偟傑偡丅 200墌亊50嶜亄180墌亊30嶜亄150墌亊40嶜亖10000墌亄5400墌亄6000墌亖21400墌 21400墌亐(50嶜亄30嶜亄40嶜)亖21400墌亐120嶜亖乹21400/120乺墌亖乹178偲1/3乺墌 偙偙偐傜偼暯嬒嶼偲屇偽傟傞柺愊恾傪巊偭偨峫偊曽偑曋棙偱偡丅  偙偺柺愊恾偼丄忋偱寁嶼偟偨1嶜乹178偲1/3乺墌偺暥廤120嶜偲丄偦偺愭偱捛壛偡傞1嶜110墌偺暥廤丠嶜傪僩乕僞儖偟偰丄暯嬒偺抣抜偑150墌偵側偭偨條巕傪昞偟偰偄傑偡丅 傾偺晹暘偺柺愊偑僀偺晹暘偵墴偟崬傑傟偰慡懱偑暯嬒壔偝傟偨偲峫偊傞偙偲偑偱偒丄傾偺柺愊偲僀偺柺愊偼摍偟偔側傝傑偡丅 傾偺柺愊乧乹28偲1/3乺墌亊120嶜亖3400墌 僀偺柺愊傕偙傟偲摍偟偄偐傜丄僀偺儓僐偺挿偝(丠墌)偼3400亐40亖85嶜 偙偺85嶜偼120嶜傪挻偊偰110墌偱嶌傞暥廤偺嶜悢偱偡丅 媮傔傞偺偼嶌傞暥廤偺憤嶜悢偩偐傜丄偙傟偵120嶜傪壛偊偰205嶜偑惓夝偲側傝傑偡丅 敀業夝摎丂1077屄 敀業夝愢 僆乕僜僪僢僋僗側夝朄偐傜徯夘偟傑偡丅夝愢(寁嶼)偺搒崌忋丄堦斣嵟屻偵2014/2014傪曗偭偰峫偊傑偡丅夝摎偱偼彍奜偟傑偡偐傜偛埨怱偔偩偝偄丅妱傜傟傞悢傪2013偵偡傞偲奺強偱寁嶼偑戝曄偱偡(丩佂丮) 栺暘偱偒傞暘悢偲偼丄暘巕偑2傑偨偼19傑偨偼53偺攞悢偵側偭偰偄傞傕偺偱偡丅 1偐傜2014偺暘巕偺偆偪丄偦傟偧傟偺攞悢偺屄悢傪峫偊傑偡丅 2偺攞悢偺屄悢乧2014亐2亖1007屄(傾) 19偺攞悢偺屄悢乧2014亐19亖106屄(僀) 53偺攞悢偺屄悢乧2014亐53亖38屄(僂) (傾)(僀)(僂)偺崌寁偼1007亄106亄38亖1151屄(A)偱偡偑丄偙偺屄悢偵偼岞攞悢偺廳暋偑偁傝傑偡丅偨偲偊偽2偲19偺岞攞悢偼(傾)偲(僀)偺椉曽偱僇僂儞僩偝傟偰偄傑偡丅 偦偙偱(A)偺屄悢偐傜岞攞悢偺屄悢傪堷偒嶼偡傞偙偲偵側傝傑偡丅 2偲19偺岞攞悢(38偺攞悢)偺屄悢乧2014亐38亖53屄(僄) 2偲53偺岞攞悢(106偺攞悢)偺屄悢乧2014亐106亖19屄(僆) 19偲53偺岞攞悢(1007偺攞悢)偺屄悢乧2014亐1007亖2屄(僇) (僄)(僆)(僇)偺崌寁偼53+19+2亖74屄偱丄偙傟傪(A)偐傜堷偔偙偙偲偱岞攞悢偺廳暋偑側偔側傝傑偡丅 1151乕74亖1077屄仼岞攞悢偺廳暋傪徚偟偨屄悢 偠偮偼偙偺堷偒嶼偵傛偭偰丄(傾)(僀)(僂)偺3幰偵嫟捠側岞攞悢偑娷傑傟側偔側偭偰偄傞偺偱偡偑丄(傾)(僀)(僂)偺3幰偵嫟捠側岞攞悢偲偼偡側傢偪2014帺恎偺偙偲偱丄栤戣偺堄恾偱偼暘巕偺2014偼彍偐傟偰偄傞偐傜丄偙偺暘(1屄)傪壛偊傞昁梫偼側偔丄忋偺1077屄偑夝摎偵側傝傑偡丅 棤媄!!! 偙偺栤戣偱偼丄栺暘偱偒側偄暘巕偺屄悢傪娙扨偵媮傔傞寁嶼幃偑桳柤偱偡丅 1乣2014偺暘巕偺偆偪丄2偺攞悢偱偼側偄悢偺懚嵼昿搙偼1/2丄19偺攞悢偱偼側偄悢偺懚嵼昿搙偼18/19丄53偺攞悢偱偼側偄悢偺懚嵼昿搙偼52/53偩偐傜丄 2014亊(1/2)亊(18/19)亊(52/53)亖936屄仼栺暘偱偒側偄暘巕偺屄悢 偙傟傪2014偐傜堷偄偰丄栺暘偱偒傞暘巕偺屄悢偼2014乕936亖1078屄偱偡丅偨偩偟偙傟偼栤戣偺堄恾偵娷傑傟側偄暘巕2014傪僇僂儞僩偟偰偄傞偐傜丄夝摎偼偝傜偵1屄傪堷偄偰1077屄偲側傝傑偡丅 (拲堄)偙偺寁嶼幃偼惵怓偺晹暘偵僆儗儞僕怓偺惍悢偺嵟彫岞攞悢傪抲偔昁梫偑偁傝傑偡丅 張弸夝摎丂40捠傝 張弸夝愢 偙偺僞僀僾偺栤戣偼彮側偄曽偵拲栚両偑巊偊傑偡丅俈屄偺僷僷僀儎偼柍帇偟偰丄俆屄偺儅儞僑乕偺暘偗曽傪峫偊傟偽夝寛偱偡丅儅儞僑乕偺暘偗曽偑寛傑傟偽丄偦傟偼摨帪偵僷僷僀儎偺暘偗曽傕寛傔偰偄傞偙偲偵側傞偺偱偡丅偩偐傜儅儞僑乕偺暘偗曽偩偗傪峫偊傟偽OK偱偡丅 傑偢係偮偺惍悢偺榓偑俆偵側傞僷僞乕儞傪峫偊偰傒傑偡丅偦偺嵺丄侾恖偑庴偗庢傞壥暔偑俁屄偱偁傞偙偲偐傜丄侽乣俁偺悢帤傪巊偆偙偲偵側傝傑偡丅 偦偺忦審壓偱丄係偮偺惍悢偺榓偑俆偵側傞僷僞乕儞偼師偺捠傝偱偡丅 傾乧(3,2,0,0) 僀乧(3,1,1,0) 僂乧(2,2,1,0) 僄乧(2,1,1,1) 師偵傾乣僄偺偦傟偧傟偵偮偄偰丄奺悢帤傪ABCD偺係恖偵妱傝摉偰傞偙偲傪峫偊傑偡丅 傾偺妱傝摉偰曽乧12捠傝(3偵側傞恖偑ABCD偺係捠傝丄偦偺偦傟偧傟偵偮偄偰2偵側傞恖偑俁捠傝偢偮丅係亊俁亖12捠傝) 僀偺妱傝摉偰曽乧傾偲摨條偵12捠傝(3偵側傞恖偑係捠傝丄0偵側傞恖偑俁捠傝) 僂偺妱傝摉偰曽乧傾偲摨條偵12捠傝(1偵側傞恖偑係捠傝丄0偵側傞恖偑俁捠傝) 僄偺妱傝摉偰曽乧係捠傝(2偵側傞恖偑ABCD偺扤偐) 仏惵偄悢帤偑儅儞僑乕傪庴偗庢傞屄悢偱丄3屄偵晄懌偡傞暘偼僷僷僀儎傪庴偗庢傞偙偲偵側傝傑偡丅傑偨丄傾乣僂偺妱傝摉偰偵嫟捠偱偡偑丄係偮偺悢帤偑仩仦仚仚傛偆偵側偭偰偄傞応崌丄仚偺偙偲偼婥偵偣偢丄仩偲仦偵側傞恖傪峫偊傟偽OK偱偡丅 埲忋傾乣僄偺崌寁偐傜丄媮傔傞夝摎偼12亊3亄4亖40捠傝偱偡丅 棫廐夝摎丂3帪娫18暘 棫廐夝愢 3偮偺強梫帪娫(12帪娫丄4帪娫丄2帪娫)偺嵟彫岞攞悢傪梡偄偰丄偙偺巇帠偺憤検傪12偲偟傑偡丅 A偝傫偺巇帠検偼1帪娫偁偨傝12亐12帪娫亖1乧傾 A偝傫B偝傫偺嫟摨嶌嬈偵偍偗傞巇帠検偼1帪娫偁偨傝12亐4帪娫亖3乧僀 B偝傫C偝傫偺嫟摨嶌嬈偵偍偗傞巇帠検偼1帪娫偁偨傝12亐2帪娫亖6乧僂丂偱偡丅 B偝傫偺1帪娫偁偨傝偺巇帠検偼僀亅傾(3亅1)傛傝2乧僄 C偝傫偺1帪娫偁偨傝偺巇帠検偼僂亅僄(6亅2)傛傝4乧僆 A偝傫C偝傫偺嫟摨嶌嬈偵偍偗傞巇帠検偼1帪娫偁偨傝傾亄僆(1+4)傛傝5丂偱偡丅 巇帠慡懱(12)偺4暘偺1偼3偱偁傝丄偦偺巇帠傪B偝傫1恖偑峴偆偲3亐2傛傝1.5帪娫偐偐傝傑偡丅巆傝偺巇帠偼9(12亅3)偱偁傝丄偦偺巇帠傪A偝傫C偝傫偺2恖偑峴偆偲丄9亐5傛傝1.8帪娫偐偐傝傑偡丅 媮傔傞夝摎偼1.5+1.8亖3.3帪娫丅巜掕偺扨埵偵捈偟偰3帪娫18暘偲側傝傑偡丅 戝弸夝摎丂29/243 戝弸夝愢 暘曣偵偼3,9,27,乧偺傛偆偵3傪偄偔偮偐偐偗嶼偟偨惍悢(3偺椵忔悢)偑彫偝偄弴偵尰傟丄暘巕偼婛栺暘悢(偦傟埲忋栺暘偱偒側偄暘悢)偵側傞惍悢偩偗偑彫偝偄弴偵尰傟偰偄傑偡丅偨偩偟丄暘巕偑暘曣傛傝彫偝偄暘悢(恀暘悢)偑懳徾偱偡丅壖暘悢偼峫偊偰偄傑偣傫丅 暘曣偑3偺婛栺恀暘悢偼栤戣偺椺帵偺傛偆偵2屄偱偡丅 暘曣偑9偺婛栺恀暘悢偼栤戣偺椺帵偺傛偆偵6屄偱偡丅 埲壓丄暘曣偑27(亖3亊3亊3)偺婛栺恀暘悢丄懕偄偰暘曣偑81(亖3亊3亊3亊3)偺婛栺恀暘悢偺屄悢傪専摙偟傑偡丅 乵暘曣偑27偺婛栺暘悢乶 1乣26偺暘巕偺偆偪丄3偺攞悢偼26亐3亖8偁傑傝2傛傝8屄偩偐傜丄婛栺暘悢偺屄悢偼26亅8亖18屄偱偡丅 仏暘巕1乣27偵偮偄偰丄3偺攞悢偼3屄偵1屄偺妱崌偩偐傜丄27亊2/3亖18屄偑婛栺暘悢偲峫偊傞偲憗偄偱偟傚偆丅 乵暘曣偑81偺婛栺暘悢乶 暘巕1乣81偵偮偄偰丄3偺攞悢偼3屄偵1屄偺妱崌偩偐傜丄81亊2/3亖54屄偑婛栺暘悢偱偡丅 偙偙傑偱偺専摙偱丄婛栺恀暘悢偺屄悢(忋偺惵悢帤偺崌寁)偼80屄偱偡丅 偟偨偑偭偰100斣栚偺暘悢偼丄暘曣偑243偺僌儖乕僾偺20斣栚偺暘悢偱偡丅 3偺攞悢傪彍奜偟偨暘巕傪暲傋偰傒傞偲丄 1,2,4,5,7,8,10,11,13,14,16,17,19,20,22,23,25,26,28,29,乧偺傛偆偵側傝丄20斣栚偺暘巕偑29偱偁傞偙偲偑傢偐傝傑偡丅媮傔傞夝摎偼29/243偱偡丅 彫弸夝摎丂44捠傝 彫弸夝愢 夝愢偺曋媂忋傾儖僼傽儀僢僩俙,俛,俠,俢,俤傪惍悢1,2,3,4,5偱抲偒姺偊丄乽5働僞偺惍悢12345偺暲傃偐偊偱丄偳偺埵偵偍偄偰傕傕偲偺惍悢(12345)偲悢帤偑堦抳偟側偄惍悢乿傪峫偊傑偡丅 乵1偮偺悢帤偩偗偑堦抳偡傞働乕僗乶 1----偺傛偆偵1偩偗偑堦抳偡傞惍悢偼 13254,13452,13524,14253,14523,14532,15234,15423,15432偺9捠傝偱偡丅摨條偵-2---丄--3--丄---4-丄----5傕奺9捠傝偱丄1偮偺悢帤偩偗偑堦抳偡傞働乕僗偼45捠傝偱偡丅 乵2偮偺悢帤偑堦抳偡傞働乕僗乶 12---偺傛偆偵2偮偺悢帤偑堦抳偡傞惍悢偼12453,12534偺2捠傝偱偡丅 12---丄1-3--側偳丄2偮偺悢帤偺堦抳僷僞乕儞偼乽5偮偺惍悢偐傜2偮偺惍悢傪慖傇慻崌偣乿偺10捠傝偱丄2偮偺悢帤偑堦抳偡傞働乕僗偼2亊10亖20捠傝偱偡丅 乵3偮偺悢帤偑堦抳偡傞働乕僗乶 123--偺傛偆偵3偮偺悢帤偑堦抳偡傞惍悢偼12354偺1捠傝偱偡丅 123--丄12-4-側偳丄3偮偺悢帤偺堦抳僷僞乕儞偼乽5偮偺惍悢偐傜3偮偺惍悢傪慖傇慻崌偣乿偺10捠傝偱丄3偮偺悢帤偑堦抳偡傞働乕僗偼1亊10亖10捠傝偱偡丅 4偮偺悢帤偑堦抳偡傞働乕僗偼偁傝傑偣傫丅仼4偮堦抳偡傟偽5偮栚傕堦抳偟偰偟傑偆偐傜 5偮偺悢帤偑堦抳偡傞惍悢(偡傋偰堦抳)偼12345偺1捠傝偱丄埲忋惵怓偺応崌偺悢傪偡傋偰壛偊丄偳偙偐偱悢帤偑堦抳偡傞惍悢偼慡晹偱45+20+10+1亖76捠傝偱偡丅 5働僞偺惍悢偺暲傃偐偊偼慡晹偱5亊4亊3亊2亊1亖120捠傝偩偐傜丄偳偺埵偵偍偄偰傕12345偲悢帤偑堦抳偟側偄惍悢偼120-76亖44捠傝偱偡丅 壞帄夝摎丂10 壞帄夝愢 乽仩暘偺俆乿亄乽俆暘偺仩乿傪暘曣(仩亊俆)偱捠暘偟偰壛偊傞偲丄乽(仩亊俆)暘偺(25亄仩亊仩)乿偲側傝傑偡丅 偙傟偑俁暘偺仮偲摍偟偄偐傜丄乽俙暘偺俛乿亖乽俠暘偺俢乿偺偲偒俙亊俢亖俛亊俠傪棙梡偟偰丄 仩亊俆亊仮亖(25亄仩亊仩)亊俁丂偡側傢偪仩亊仮亊俆亖75亄仩亊仩亊俁偲側傝傑偡丅 偙偺幃偺嵍曈僆儗儞僕晹暘偼俆偺攞悢偱丄塃曈偺僆儗儞僕晹暘75傕俆偺攞悢偩偐傜丄惵偄晹暘傕俆偺攞悢偵側傜側偔偰偼側傝傑偣傫丅 仏俆偺攞悢偵偼俆偺攞悢傪壛偊側偄尷傝俆偺攞悢偵偼側傜側偄両 偙偺帪揰偱仩偑俆偺攞悢偱偁傞偙偲偑妋掕偟傑偡丅 仩亖俆偺偲偒丄乽俆暘偺俆乿亄乽俆暘偺俆乿亖乽俁暘偺俇乿偲側傝傑偡偑丄偙偺応崌偼仮偑俁偺攞悢偲側傝忦審偵斀偟傑偡丅 仩亖10偺偲偒丄乽俆暘偺10乿亄乽10暘偺俆乿偼乽俁暘偺仮(惍悢)乿偱昞偡偙偲偑偱偒傑偣傫丅 仩亖15偺偲偒丄乽15暘偺俆乿亄乽俆暘偺15乿亖乽俁暘偺10乿偲側偭偰戣堄傪枮偨偟傑偡丅 鋳庬夝摎丂俉恖 鋳庬夝愢丂  仏恾拞偺怓偮偒悢帤偼偡傋偰斾傪昞偡悢帤偱偡丅幚悢偱偼偁傝傑偣傫丅(12屄偺傒幚悢) 弶傔偵偁偭偨敀嬍偲愒嬍偺屄悢偺斾傪僆儗儞僕丄巕嫙偨偪偵攝偭偨敀嬍偲愒嬍偺屄悢偺斾傪惵偺悢帤偱帵偟傑偟偨丅偡傞偲敀嬍偺屄悢偵偮偄偰僆儗儞僕偺斾偱俀丄惵偺斾偱俈偩偐傜丄偙傟傜傪嵟彫岞攞悢偺14偵摑堦偟傑偡丅仼僆儗儞僕斾偼俈攞丄惵斾偼俀攞 摑堦屻偺斾傪僌儕乕儞偱帵偟傑偟偨丅僌儕乕儞偺斾偺俁偑12屄偩偐傜丄僌儕乕儞偺斾偺侾偼4屄丄僌儕乕儞偺斾偺14(弶傔偵偁偭偨敀嬍偺屄悢)偼係亊14亖56屄偱偡丅敀嬍偼俈屄偢偮攝偭偨偐傜丄巕嫙偺恖悢偼56亐俈亖俉恖偱偡丅 彫枮夝摎丂俙7亾丄俛11亾 彫枮夝愢丂 仏恾偺悢抣偼忋抜偐傜弴偵擹搙丄怘墫悈偺廳偝丄怘墫偺廳偝偱偡丅嵟廔揑側寢壥傪偡傋偰婰擖偟偰偄傑偡偐傜丄夝愢偺棳傟偵増偭偰偛妋擣偔偩偝偄丅  怘墫悈慡懱偺廳偝偼丄俙400g仺200g仺600g丄俛600g仺800g仺400g偺傛偆偵曄壔偟傑偡丅 乽嵟屻偺俙乿乽嵟屻偺俛乿偺擹搙偼俙9亾丄俛10亾偩偐傜丄嵟廔揑側怘墫偺廳偝偼俙600亊0.09=54g丄俛400亊0.1=40g偱偡丅傑偨乽曄壔屻俛乿乽堏偟偨俛乿乽嵟屻偺俛乿偼偡傋偰摨偠擹搙偱偡丅 乽堏偟偨俛乿偲乽嵟屻偺俛乿偼摨偠撪梕偱偡丅仺乽曄壔屻俛乿偺敿暘傪俙偵堏偟偨偐傜 乽巆傝偺俙乿偲乽堏偟偨俛乿偺崿崌偱乽嵟屻偺俙乿偑偱偒傞偐傜丄乽巆傝偺俙乿偵娷傑傟傞怘墫偼54亅40亖14g偱乽巆傝偺俙乿偺擹搙偼14亐200=0.07=7亾偱偡丅偙傟偼乽嵟弶偺俙(夝摎)乿乽堏偟偨俙乿偲摨偠擹搙偱偡丅 乽堏偟偨俙乿偲乽巆傝偺俙乿偼摨偠撪梕偱偡丅仺乽嵟弶偺俙乿偺敿暘傪俛偵堏偟偨偐傜 乽堏偟偨俙乿偲乽嵟弶偺俛乿偺崿崌偱乽曄壔屻俛乿偑偱偒傞偐傜丄乽嵟弶偺俛乿偵娷傑傟傞怘墫偼800亊0.1亅14亖80亅14=66g偱乽嵟弶偺俛乿偺擹搙偼66亐600=0.11=11亾偱偡丅 棫壞夝摎丂(1)16捠傝丂(2)17暘36昩 棫壞夝愢丂(1)僄儗儀乕僞乕偺忋徃偵偮偄偰丄6奒偐傜11奒傑偱5奒暘偺忋徃偑昁梫偱偡丅僄儗儀乕僞乕偺掆巭偵偮偄偰丄嵟掅1夞(嵟屻偺11奒偩偗)偐傜嵟崅5夞(7奒偐傜11奒偺偡傋偰)偺掆巭偑峫偊傜傟傑偡丅 仏11奒偱偲傃傜偑暵傑偭偰偄傞偙偲偐傜丄11奒偺掆巭偼昁偢娷傑傟傑偡丅 掆巭偟偨夞悢偵傛偭偰応崌暘偗傪偟偰傒傑偡丅 傾(1夞掆巭偟偨応崌)丂11奒偱掆巭偟偨1捠傝偱偡丅 僀(2夞掆巭偟偨応崌)丂11奒偺懠偵偁偲1偮偺奒傪慖傃傑偡丅7奒乣10奒偺4捠傝偱偡丅 僂(3夞掆巭偟偨応崌)丂11奒偺懠偵偁偲2偮偺奒傪慖傃傑偡丅7奒乣10奒偺4偮偺奒偺拞偐傜2偮偺奒傪慖傇偐傜6捠傝偱偡丅 僄(4夞掆巭偟偨応崌)丂11奒偺懠偵偁偲3偮偺奒傪慖傃傑偡丅7奒乣10奒偺4偮偺奒偺拞偐傜3偮偺奒傪慖傇偐傜4捠傝偱偡丅 僆(5夞掆巭偟偨応崌)丂7奒偐傜11奒偺偡傋偰偺奒偱掆巭偟傑偡丅1捠傝偱偡丅 傾乣僆傪崌寁偟偰丄媮傔傞夝摎偼16捠傝偱偡丅 (2)5奒暘偺忋徃帪娫30昩(亖6昩亊5)偵偮偄偰偼丄(1)偺偳偺応崌傕摨偠偱偡丅偙傟傜偺崌寁偱30昩亊16捠傝亖480昩偱偡丅 掆巭帪娫偼傾丄僀丄僂丄僄丄僆偺弴偵12昩丄24昩丄36昩丄48昩丄60昩偱偡丅偙傟傜偵(1)偱峫偊偨僷僞乕儞悢傪偐偗偰崌寁偡傞偲丄 12昩亊1捠傝亄24昩亊4捠傝亄36昩亊6捠傝亄48昩亊4捠傝亄60昩亊1捠傝 亖12昩亄96昩亄216昩+192昩+60昩亖576昩偱偡丅 媮傔傞夝摎偼480昩+576昩亖1056昩亖17暘36昩偱偡丅 崚塉夝摎丂[6恖晹壆]6幒丂[7恖晹壆]4幒丂[8恖晹壆]7幒 崚塉夝愢丂廂梕掕堳偲幚嵺偺廂梕偱8恖晹壆偺巊偄曽偵堘偄偼側偄偐傜丄130恖偲120恖偺嵎偺10恖偼6恖晹壆偲7恖晹壆偺廂梕偱惗偠傞偙偲偑傢偐傝傑偡丅6恖晹壆傪仩晹壆丄7恖晹壆傪仮晹壆偲偡傞偲丄(傾)6亊仩亄7亊仮偲(僀)7亊仩亄8亊仮偺嵎偑10恖偱偡丅(僀)偼(傾)傛傝仩偲仮偑1屄偢偮懡偄偐傜仩亄仮亖10乧(僂)偱偁傞偙偲偑傢偐傝傑偡丅仏(僀)偐傜(傾)傪堷偄偨偲峫偊偰傕傛偄偱偡 忦審偐傜偡傋偰偺晹壆偺崌寁悢偼17幒偩偐傜丄8恖晹壆偼17亅10亖7幒偱偡丅仏慡懱偺晹壆悢偐傜6恖晹壆丄7恖晹壆偺崌寁悢(仩亄仮)傪堷偄偨 廂梕掕堳偺忦審偱丄6亊仩亄7亊仮亄8亊7亖120丂嵍曈偺56(8亊7)傪塃曈偐傜堷偄偰 6亊仩亄7亊仮亖64乧(僄)偱偡丅偁偲偼(僂)偲(僄)傪巊偭偰偮傞偐傔嶼(傑偨偼徚嫀嶼)傪夝偔偲丄仩亖6幒丄仮亖4幒偱偁傞偙偲偑傢偐傝傑偡丅 惔柧夝摎丂2025擭 惔柧夝愢丂偁傞擔晅偲侾擭屻偺摨偠擔晅偼梛擔偑1偮愭偵僘儗傑偡丅偨偩偟丄偁傞擔晅偲1擭屻偺摨偠擔晅偺娫偵偆傞偆擭(尨懃偼惣楋偑4偺攞悢丅100偺攞悢偼彍奜丄400偺攞悢偼嵞嶼擖偺椺奜偁傝)偺2/29偑偁傞応崌偼梛擔偑2偮愭偵僘儗傑偡丅 2014擭偐傜偺4寧5擔偺梛擔偼埲壓偺捠傝偱偡丅愒偄暥帤偺偲偙傠偑慜擭偐傜偺宱夁偱偆傞偆擭偺2/29傪捠夁偟丄梛擔偑2偮愭偵僘儗偨偲偙傠偱偡丅 2014 搚仺2015 擔仺2016 壩仺2017 悈仺2018 栘仺2019 嬥仺2020 擔仺2021 寧仺2022 壩仺2023 悈仺2024 嬥仺2025 搚 弔暘夝摎丂880屄 弔暘夝愢丂3働僞偺惍悢偺奺埵偺悢帤偺榓偼嵟彫偑1(仺1+0+0)偱嵟戝偑27(仺9+9+9)偩偐傜丄奺埵偺悢帤偺榓偑24傛傝彫偝偄惍悢傛傝傕丄媡偵24埲忋偵側傞惍悢偺曽偑彮側偔偰悢偊傗偡偄偙偲偑梊憐偱偒傑偡丅偟偨偑偭偰奺埵偺悢帤偺榓偑24埲忋偵側傞3偮偺悢帤偺慻崌偣傪峫偊丄師偵暲傃偐偊傪峫偊偰傒傑偡丅 偙偺偲偒丄5埲壓偺悢帤偼巊偆偙偲偑偱偒傑偣傫丅側偤側傜5傪巊偆偲巆傝2偮偺悢帤傪9偵偟偰傕9+9+5=23傛傝丄榓偑24偵枮偨側偄偐傜偱偡丅 榓偑24埲忋偵側傞3偮偺惍悢偺慻傒崌傢偣傪昐偺埵亞廫偺埵亞堦偺埵偵側傞傛偆偵峫偊傞偲丄傾999丄僀998丄僂997丄僄996丄僆988丄僇987丄僉888偺僷僞乕儞偑峫偊傜傟傑偡丅 偙偺偆偪傾偲僉偵偼暲傃偐偊偑側偔(奺1捠傝)丄僀僂僄僆偼奺3捠傝偢偮偺暲傃偐偊偑偁傝(偨偲偊偽僀偼998,989,899)丄僇偵偼3亊2亊1亖6捠傝偺暲傃偐偊偑偁傝傑偡丅 偙傟傜傪崌寁偟偰丄奺埵偺悢帤偺榓偑24埲忋偵側傞3働僞偺惍悢偼慡晹偱1亊2+3亊4亄6亖20屄偱偡丅 3働僞偺惍悢偼慡晹偱900屄(100乣999)偁傝丄偄傑媮傔偨20屄埲奜偼偡傋偰奺埵偺悢帤偺榓偑24傛傝彫偝偔側傝傑偡丅媮傔傞夝摎偼900-20亖880屄偱偡丅 孾瀛夝摎丂16317 孾瀛夝愢丂奩摉偡傞惍悢傪師偺傛偆偵惍棟偟偰傒傑偡丅夝愢昞婰偺僶儔儞僗偱丄2働僞偺惍悢66傪066偲偟偰偄傑偡丅 66仭偺僞僀僾仺9屄丅660丄661丄662丄663丄664丄665丄667丄668丄669 6仭6偺僞僀僾仺9屄丅606丄616丄626丄636丄646丄656丄676丄686丄696 仭66偺僞僀僾仺9屄丅066丄166丄266丄366丄466丄566丄766丄866丄966 昐偺埵偵6偑尰傟傞偺偼18夞偱崌寁偼600亊18乧傾 廫偺埵偵6偑尰傟傞偺偼18夞偱崌寁偼60亊18乧僀 堦偺埵偵6偑尰傟傞偺偼18夞偱崌寁偼6亊18乧僂 傑偨丄6埲奜偺悢帤偼偳傟傕昐丄廫丄堦偺埵偵1夞偢偮尰傟傞偐傜丄崌寁偼111+222+333+444+555+777+888+999亖111亊(1+2+3+4+5+7+8+9)亖111亊39乧僄 傾丄僀丄僂偺崌寁偼(600+60+6)亊18亖666亊18亖111亊6亊18亖111亊108 偙傟偵僄傪壛偊偰丄媮傔傞夝摎偼111亊(108+39)亖111亊147亖16317偱偡丅 拲堄丂666偼彍奜偟偰偄傑偡丅6偑3屄弌偰偔傞666傪丄6偑2屄弌偰偔傞悢偵娷傔傞偲偄偆棟孅傕姰慡側娫堘偄偱偼側偄偲巚偄傑偡偑丄嶼悢偱偼彍奜偡傞敾抐偑晛捠偩偲巚偄傑偡丅 塉悈夝摎丂44捠傝 塉悈夝愢丂1丄2丄3偺惍悢偺懌偟嶼偱榓傪7偵偡傞幃傪峫偊傑偡丅傾乧1+1+1+1+1+1+1丂僀乧1+1+1+1+1+2丂僂乧1+1+1+1+3丂僄乧1+1+1+2+2丂僆乧1+1+2+3丂僇乧1+2+2+2丂僉乧1+3+3丂僋乧2+2+3丂師偵偙傟傜偺暲傃懼偊傪峫偊傞偲丄傾乧1捠傝(暲傃懼偊僫僔)丂僀乧6捠傝(2偺埵抲偑6儢強)丂僂乧5捠傝(3偺埵抲偑5儢強)丂僄乧10捠傝(5儢強偐傜2偺埵抲傪2儢強慖傇慻崌偣仺5亊4亐2)丂僆乧12捠傝(4儢強偺偆偪2偺埵抲偑4捠傝丄3偺埵抲偑3捠傝仺4亊3)丂僇乧4捠傝(1偺埵抲偑4儠強)丂僉乧3捠傝(1偺埵抲偑3儠強)丂僋乧3捠傝(3偺埵抲偑3儠強)丂偙傟傜傪壛偊偰丄戣堄偺応崌偺悢偼慡晹偱44捠傝偱偡丅 棫弔夝摎丂742 棫弔夝愢丂12傪壛偊傞偲13偱妱傝愗傟傞惍悢偲偼13偺攞悢傛傝1戝偒偄惍悢偱偡丅摨條偵18傪壛偊傞偲19偱妱傝愗傟傞惍悢偲偼19偺攞悢傛傝1戝偒偄惍悢偱偡丅偙傟傜2偮偺忦審傪偲傕偵枮懌偝偣傞惍悢偲偼乽13偲19偺岞攞悢傛傝1戝偒偄惍悢乿偱偁傝丄13偲19偺嵟彫岞攞悢偑247偱偁傞偙偲偐傜丄媮傔傞惍悢偺岓曗偼乲247偺攞悢傛傝1戝偒偄惍悢乧仛乴偱偡丅 仛偵偁偰偼傑傞3働僞偺惍悢偼247亄1亖248丄247亊2亄1亖495丄247亊3亄1亖742丄247亊4亄1亖989偺4捠傝偑峫偊傜傟傑偡偑丄偙偺偆偪乽昐偺埵偲堦偺埵偺悢帤傪擖傟偐偊傞偲傕偲偺悢傛傝彫偝偔側傞乿偲偄偆忦審傪枮偨偡偺偼742偩偗偱偡丅 戝姦夝摎丂53捠傝 戝姦夝愢丂5墌嬍2枃偲10墌嬍1枃偺嬥妟偑摍偟偔側傞偐傜丄偦偺廳暋傪徚偡偨傔偵10墌嬍3枃傪5墌嬍6枃偵椉懼偟丄1墌嬍2枃丄5墌嬍8枃丄50墌嬍1枃偲偟偰峫偊傑偡丅1墌嬍偺巊偄曽偼0枃偐1枃偐2枃偺3捠傝乧傾丂5墌嬍偺巊偄曽偼0枃乣8枃偺9捠傝乧僀丂50墌嬍偺巊偄曽偼0枃偐1枃偺2捠傝乧僂丂偱偡丅傾丄僀丄僂傛傝3庬椶偺峝壿偺慻傒崌傢偣曽偼慡晹偱3亊9亊2亖54捠傝偱偡丅偙偺偆偪1捠傝偼3庬椶偺峝壿偑[0枃-0枃-0枃]偺応崌偩偐傜丄偦偺1捠傝傪彍奜偟偰丄媮傔傞夝摎偼53捠傝偲側傝傑偡丅 彫姦夝摎丂9丄12丄15丄17 彫姦夝愢丂4偮偺惍悢傪彫偝偄弴偵A丄B丄C丄D偲偟傑偡丅2偮偺惍悢偺榓偑傕偭偲傕彫偝偔側傞偺偼A+B亖21乧傾丄2斣栚偵彫偝偔側傞偺偼A+C亖24乧僀丄傑偨丄2斣栚偵戝偒偔側傞偺偼B+D亖29乧僂丄傕偭偲傕戝偒偔側傞偺偼C+D亖32偱偡丅偙偙偱枹妋掕偺B+C偲A+D偲偵偮偄偰峫偊傞偲丄傾丄僀傛傝B偲C偺嵎偑3(亖24乕21)偱婏悢偩偐傜丄嵎偑婏悢側傜榓傕婏悢偵側傝B+C亖27丅巆傞C+D亖26偱偡丅 B偲C偼乵嵎偑3丄榓偑27乶偩偐傜榓嵎嶼傪梡偄偰B亖12丄C亖15丅B亖12傪傾偵偁偰偼傔偰A亖9丄僂偵偁偰偼傔偰D亖17偱偡丅偙偺夝摎偼丄4偮偺偆偪1偮偩偗偑嬼悢偲偄偆忦審偵傕晞崌偟偰偄傑偡丅 搤帄夝摎丂33帪娫 搤帄夝愢丂偁傞巇帠慡懱傪1偲偟傑偡丅B1恖(扨撈帪)偑俇帪娫偐偐偭偨巇帠偼1乕(2/5+13/30)亖1/6偩偐傜丄B1恖(扨撈帪)偑1帪娫偱廔偊傞巇帠偼1/6亐6亖1/36偱偡丅嫟摨嶌嬈帪偺B偼擻椡偑俀妱憹偟偩偐傜丄嫟摨嶌嬈帪偺B偑1帪娫偱廔偊傞巇帠偼1/36仏1.2(暘悢偱偼6/5)亖1/30偱偡丅A,B2恖偑俇帪娫偱廔偊偨2/5偺巇帠偺偆偪丄1/30仏6亖1/5偼B偑峴偭偨暘偩偐傜丄A偑峴偭偨暘傕摍偟偔1/5偱偁傝(2/5乕1/5)丄嫟摨嶌嬈帪偺A偑1帪娫偱廔偊傞巇帠傕1/5亐6亖1/30偱偡丅偙傟偼A1恖(扨撈帪)偺侾妱憹偟偩偐傜丄A1恖(扨撈帪)偑1帪娫偱廔偊傞巇帠偼1/30亐1.1(暘悢偱偼11/10)亖1/33偱偡丅偟偨偑偭偰丄偁傞巇帠慡懱傪A1恖偑峴偆偲1亐1/33亖33帪娫偐偐傝傑偡丅 戝愥夝摎丂1帪娫48暘 戝愥夝愢丂峴偒偼乽恑傓亄媥傓乿偱45暘偺僙僢僩丅206暘(3帪娫26暘)亐45暘亖4偁傑傝26暘傛傝丄40暘4夞偲偁傑傝偺26暘傪崌寁偟偨186暘偑恑傫偩帪娫丅婣傝偼懍偝偑2攞偩偐傜恑傓帪娫偼峴偒偺1/2偵側傝丄186暘亐2亖93暘丅婣傝偼30暘恑傫偱5暘媥傓偐傜丄30暘-5暘-30暘-5暘-30暘-5暘偱35暘亊3亖105暘丅偙偺偁偲3暘恑傓偲恑傫偩帪娫偑93暘偵側傞丅婣傝偺強梫帪娫偼105暘亄3暘亖108暘亖1帪娫48暘丅 彫愥夝摎丂57.6亐4.5 彫愥夝愢丂屻敿偺傢傝嶼偺彜偑12.8偩偐傜丄慜敿偺傢傝嶼偺侾偺埵傑偱偺彜偼12偺偼偢偱偡丅 乹慜敿乺仩亐仮亖12偁傑傝3.6丂仺丂仩亖仮亊12+3.6 乹屻敿乺仩亐仮亖12.8丂仺丂仩亖仮亊12.8亖仮亊12+仮亊0.8丂(暘攝朄懃偱12.8傪暘偗偨) 壓慄晹暘偑摍偟偄偐傜丄仮亊0.8亖3.6傛傝仮亖4.5丂仩亖4.5亊12.8亖57.6 |