 夁嫀栤PART2 |
棫壞 師偺傛偆偵丄俁偺攞悢偲俈偺攞悢傪彍偄偨惍悢偺悢楍傪嶌傝傑偡丅 侾丄俀丄係丄俆丄俉丄10丄11丄乧乧乧 惍悢2015偼偙偺悢楍偺壗斣栚偺惍悢偱偡偐丠 崚塉 俆偲俇偺椉曽丄傑偨偼曅曽偩偗偺悢傪偄偔偮偐偨偟偰悢傪嶌傝傑偡丅俆偲俇傪俆亄俆亄俇亄俇亄俇亖28丄俆亄俆亄俆亄俆亖20偺傛偆偵壗夞巊偭偰傕傛偄偲偡傞偲偒丄嶌傞偙偲偑偱偒側偄10傛傝戝偒偄惍悢傪偡傋偰媮傔偰偔偩偝偄丅 惔柧 塃偺恾偼戜宍偺拞偵2杮偺懳妏慄傪堷偄偨傕偺偱偡丅傽偺晹暘(巐妏宍)偺柺愊偑37cm2偺偲偒丄仩偺挿偝偼壗cm偱偟傚偆偐丠 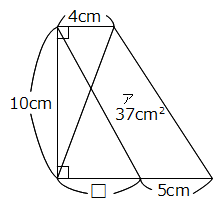 弔暘 壓偺恾偼柺愊48cm2偺惓曽宍傪4偮偺晹暘傽丄傿丄僁丄僃偵暘偗偨傕偺偱偡丅傽偺柺愊偑8cm2丄傿偺柺愊偑12cm2偺偲偒丄僃偺柺愊傪媮傔偰偔偩偝偄丅 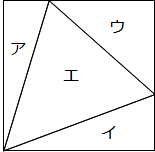 孾瀛 僆儗儞僕偲敀偺惓曽宍偺僞僀儖傪丄偁傞婯懃偵偟偨偑偭偰壓偺恾偺傛偆偵惓曽宍偵暲傋偰偄偒傑偡丅敀偄僞僀儖傪112枃巊偭偰偱偒傞惓曽宍偼壗斣栚偱偟傚偆偐丠 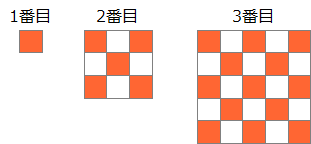 塉悈 俀偮偺惍悢俙偲俛偵偮偄偰師偺傾丄僀丄僂偑傢偐偭偰偄傑偡丅 傾丂1偐傜2000傑偱偵俙偺攞悢偼19屄偁傝傑偡丅 僀丂1偐傜2000傑偱偵24偲俛偺岞攞悢偼27屄偁傝傑偡丅 僂丂1偐傜2000傑偱偵俙偲俛偺岞攞悢偼俇屄偁傝傑偡丅 峫偊傜傟傞俙偲俛偺慻傪偡傋偰媮傔偰偔偩偝偄丅 棫弔 崱愹孨偼10亾偺怘墫悈傪100倗嶌傞偮傕傝偱偟偨偑丄娫堘偊偰悈100倗偵怘墫10倗傪梟偐偟偰偟傑偄傑偟偨丅娫堘偄偵婥偯偄偨崱愹孨偼丄怘墫悈傪偁傞検偩偗幪偰丄偦偺屻怘墫傪偁傞検偩偗梟偐偟偰10亾偺怘墫悈100倗傪嶌傝捈偟傑偟偨丅 崱愹孨偑幪偰偨怘墫悈偺廳偝(倗)偲丄偦偺屻壛偊偨怘墫偺廳偝(倗)傪媮傔偰偔偩偝偄丅 棫壞夝摎丂1152斣栚 棫壞夝愢 3偲7偺嵟彫岞攞悢21傑偱傪彂偒弌偟偰傒傑偡丅 侾丄俀丄係丄俆丄俉丄10丄11丄13丄16丄17丄19丄20乧傽 偙偺傛偆偵12屄偺惍悢偑奩摉偟傑偡丅 摨條偵42(亖3偲7偺2斣栚偺岞攞悢)傑偱偺斖埻偱傕摨偠傛偆偵12屄偺惍悢偑奩摉偟傑偡丅 22丄23丄25丄26丄29丄31丄32丄34丄37丄38丄40丄41乧僀 偙傟傜偺惍悢偼偡傋偰傾偺12屄偵21傪壛偊偨惍悢偱偡丅 偙偺傛偆偵3偺攞悢偲7偺攞悢傪彍偄偨悢楍偲偼丄3偲7偺岞攞悢偛偲偵嬫愗偭偨斖埻偺拞偵昁偢12屄偢偮懚嵼偟傑偡丅 2015亐21亖95偁傑傝20傛傝丄惍悢2015偼21偺攞悢(亖3偲7偺岞攞悢)傛傝1彫偝偔丄 2015偼傾偺20丄僀偺41偺傛偆偵僌儖乕僾12屄偺嵟屻偵尰傟傞惍悢偱偡丅 仏1傪壛偊傞偲21偺攞悢偵側傞惍悢偲峫偊偰傕傛偄偱偟傚偆丅偨偲偊偽僀偺嵟屻偺41偵1傪壛偊傞偲42丅偙傟傪21偱妱傞偲2偵側傝丄僀偺41偼2慻栚偺僌儖乕僾偺嵟屻偺惍悢偱偁傞偙偲偑傢偐傝傑偡丅 (2015亄1)亐21亖2016亐21亖96傛傝丄2015偼96慻栚偺僌儖乕僾偺嵟屻偺惍悢偱偡丅 偟偨偑偭偰2015偼戣堄偺悢楍偵偍偄偰丄96亊12亖1152斣栚偵尰傟傑偡丅 崚塉夝摎丂13偲14偲19 崚塉夝愢 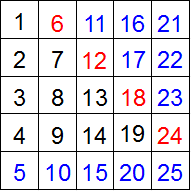 忋偺傛偆偵悢帤傪俆偮偢偮暲傋偨昞傪嶌偭偰峫偊傑偡丅 堦斣壓偺抜偼俆偺攞悢偩偐傜丄俆偺偨偟嶼偱昞尰偡傞偙偲偑偱偒傑偡丅 仺昞尰偱偒傞惍悢偼惵怓 偦傟埲奜偺抜偼丄嵍偐傜尒偨偲偒偵堦搙俇偺攞悢偑尰傟傞偲丄偦偺悢傪娷傔丄偦傟傛傝塃懁偼偡傋偰昞尰偡傞偙偲偑偱偒傑偡丅側偤側傜奺抜偺悢帤偼俆偢偮憹偊偰偄偔偐傜丄 偨偲偊偽23亖俇+俇+俇+俆偺傛偆側梫椞偱偡丅 偮傑傝俆偲俇偺偨偟嶼偱昞尰偡傞偙偲偑偱偒側偄偺偼丄忋偐傜係抜偱丄俇偺攞悢傛傝嵍懁偵偁傞惍悢偱偡丅栤戣偺忦審偵乽10傛傝戝偒偄乿偲偁傞偐傜丄夝摎偼13丄14丄19偲側傝傑偡丅 惔柧夝摎丂6cm 惔柧夝愢 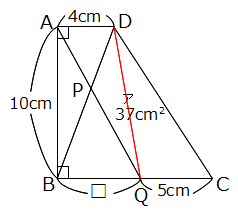 忋偺恾偺傛偆側曗彆慄DQ傪彂偒擖傟偰峫偊傑偡丅 仮AQD偼掙曈4cm崅偝10cm偩偐傜丄柺愊偼20cm2偱偡丅乧嘆 傑偨丄仮DQC偼掙曈5cm丄崅偝10cm偩偐傜柺愊偼25cm2偱偡丅 栤戣偺忦審偐傜傽偺柺愊偑37cm2偩偐傜丄仮DPQ亖37亅25亖12cm2偱偡丅乧嘇 嘆丄嘇傛傝仮APD亖20亅12亖8cm2乧嘊 嘇丄嘊傛傝丄仮APD丗仮DPQ亖8:12亖2:3偲傢偐傝丄偙偺柺愊斾偼慄暘斾AP:PQ偲堦抳偟傑偡丅 仏崅偝偑摍偟偄嶰妏宍偼(掙曈偺斾)亖(柺愊斾) 仮APD偲仮QPB偼憡帡偺娭學偑偁傝丄AD:QB偼AP:PQ偲摍偟偔2:3偱偡丅AD亖4cm偩偐傜丄BQ亖4亊3/2亖6cm偱偡丅 弔暘夝摎丂20cm2 弔暘夝愢 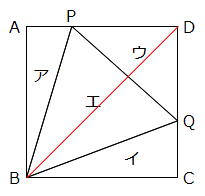 塃偺恾偺傛偆側懳妏慄傪彂偒擖傟偰峫偊傑偡丅 塃偺恾偺傛偆側懳妏慄傪彂偒擖傟偰峫偊傑偡丅埲壓丄柺愊偺扨埵cm2傪徣偄偰夝愢偟傑偡丅 仮ABD偼惓曽宍偺敿暘偩偐傜48亐2亖24丄傽偼8偩偐傜仮PBD偼24亅8亖16偱偡丅 仮ABP(傽)偲仮PBD偼崅偝偑摍偟偄偐傜丄掙曈偺斾偼柺愊偺斾偲摍偟偔AP:PD亖8:16亖1:2偱偡丅 摨偠傛偆偵仮DBC偑惓曽宍偺敿暘偱24丄僀偑12偩偐傜丄仮DBQ偼24亅12亖12丅傛偭偰DQ:QC偼仮DBQ偲仮QBC(僀)偺柺愊斾偐傜12:12亖1:1偱偡丅 偙傟傜偺偙偲傪棙梡偟偰奺慄暘傪嬶懱揑側惍悢偱昞偟偰偍偒傑偡丅偨偲偊偽惓曽宍偺1曈傪6偲偡傞偲丄AP亖2丄PD亖4丄DQ亖QC亖3偱偡丅 傾偲僁偺柺愊偼[掙曈亊崅偝]偺偐偗嶼傪偟偰丄傽:僁亖(AB亊AP):(PD亊QC)亖(6亊2):(4亊3)亖12:12亖1:1丅偮傑傝傽偲僁偺柺愊偼摍偟偄偙偲偑傢偐傝傑偡丅仺傾偺柺愊偑8偩偐傜丄僂偺柺愊傕8 僃偺柺愊偼惓曽宍慡懱偐傜傽丄僀丄僂傪堷偄偰丄48亅(8+8+12)亖20偲媮傔傞偙偲偑偱偒傑偡丅 仏傽偲僁偺柺愊斾傪掙曈亊崅偝偱媮傔傞偺偑億僀儞僩偱偡丅夝愢偱偼惓曽宍偺1曈傪6偲偟傑偟偨偑丄奺強偺斾偑偒偪傫偲斀塮偝傟偰偄傟偽丄偳偺傛偆側悢抣偱峫偊偰傕摨偠柺愊斾偑媮傔傜傟傑偡丅傑偨丄嶰妏宍偺柺愊偺岞幃偼掙曈亊崅偝亐2偱偡偑丄亐2偵娭偟偰偼柺愊斾偺嶼弌偱偼晄梫偱偟傚偆(峴偭偰傕峔偄傑偣傫偑乧)丅 孾瀛夝摎丂俉斣栚 孾瀛夝愢 偳偺恾偵偍偄偰傕僆儗儞僕怓偺僞僀儖偼敀偄僞僀儖傛傝侾枃懡偔丄傑偨僞僀儖偺崌寁枃悢偼1斣栚1亊1亖1丄2斣栚3亊3亖9丄3斣栚5亊5亖25偺傛偆偵婏悢亊婏悢偺暯曽悢偱偡丅 敀偄僞僀儖偑112枃偺偲偒丄僆儗儞僕怓偺僞僀儖偼113枃偩偐傜丄僞僀儖偺崌寁枃悢偼112亄113亖225枃偵側傝丄225(暯曽悢)亖15亊15偱偡丅仺惓曽宍偺1曈偑15枃偲傢偐傞 仩(斣栚)亊2亅1亖(惓曽宍偺1曈偺枃悢)偺娭學偑偁傞偐傜丄偙偺娭學傪巊偭偰媡嶼偡傞偲 (15亄1)亐2亖8傛傝丄媮傔傞夝摎偼8斣栚偱偡丅 塉悈夝摎丂(俙,俛) 亖 (102,9) (102,18) (105,9) 塉悈夝愢丂 惍悢1偐傜俶傑偱偵娷傑傟傞俹偺攞悢偺屄悢偼俶亐俹偺彜偺惍悢晹暘偱偡(偁傑傝偼柍帇偟偰傛偄)丅 忦審傾偐傜2000亐俙偺彜偼19埲忋20枹枮偱偡丅偙偺忦審傪枮偨偡俙偺抣傪峫偊丄俙偺岓曗偼101丄102丄103丄104丄105偱偡丅乧嘆 24偲俛偺嵟彫岞攞悢傪仩偲偡傞偲丄忦審僀偐傜2000亐仩偺彜偼27埲忋28枹枮偱偡丅偙偺忦審傪枮偨偡仩偺抣傪峫偊丄仩偺岓曗偼72丄73丄74偲側傝傑偡偑丄仩偼24偺攞悢偩偐傜72偵寛掕偟傑偡丅仺24偲俛偺嵟彫岞攞悢仩偼72 偙偺偙偲傪巊偭偰戞38島嵗偱夝愢偟偨庤弴傪梡偄傞偲俛偺岓曗偼9丄18丄36丄72偲傢偐傝傑偡丅乧嘇 俙偲俛偺嵟彫岞攞悢傪仮偲偡傞偲丄忦審僂偐傜2000亐仮偺彜偼6埲忋7枹枮偱偡丅偙偺忦審傪枮偨偡仮偺抣傪峫偊丄仮偺岓曗偼286埲忋333埲壓偱偡丅乧嘊 俙(嘆)丄俛(嘇)偺岓曗傪慻傒崌傢偣丄嘊偺忦審傪枮偨偡(俙,俛)偺慻傪挷傋傑偡丅 [俙偑101丄103偺応崌] 101丄103偼慺悢偩偐傜丄俛偺偡傋偰偺岓曗偲屳偄偵慺偵側偭偰偟傑偄丄嵟彫岞攞悢偑嘊偺斖埻偵廂傑傝傑偣傫丅 [俙偑102偺応崌] 俛傪9傑偨偼18偲偟偨偲偒丄嵟彫岞攞悢偑306偲側傝忦審嘊傪枮偨偟傑偡丅仺夝摎2慻Get! [俙偑104偺応崌] 俛亖9偲偼屳偄偵慺偱晄揔丄俛亖18丄36丄72偲偼岞栺悢傪帩偪傑偡偑丄偳偺応崌傕嵟彫岞攞悢偑嘊偺斖埻偵廂傑傝傑偣傫丅 [俙偑105偺応崌] 俛傪9偲偟偨偲偒丄嵟彫岞攞悢偑315偲側傝忦審嘊傪枮偨偟傑偡丅仺夝摎1慻Get! 埲忋慡晹偱3慻偺夝摎偑峫偊傜傟傑偡丅嵟彫岞攞悢偺寁嶼偼偡偩傟幃偺昅嶼偑桳柤偱偡偑丄偁傢偣偰戞38島嵗偺抦幆偑偁傞偲丄偙偺傛偆側栤戣偵墳梡偑偒偔偲巚偄傑偡丅 棫弔夝摎丂幪偰偨怘墫悈11倗丂偦偺屻壛偊偨怘墫侾倗 棫弔夝愢丂 10亾偺怘墫悈傪嶌傞偨傔偵偼丄怘墫10倗偵懳偟偰丄悈傪100倗偱偼側偔90倗崿偤傟偽傛偄傢偗偱偡丅仺崱愹孨偺弶傔偺憖嶌偼悈偑10倗懡偡偓偨 嘆 傑偢悈傪10倗尭傜偡偙偲傪峫偊傑偡丅 崱愹孨偑弶傔偵娫堘偊偰嶌偭偨怘墫悈偺擹搙偼10/110亖1/11偩偐傜丄悈偑愯傔傞妱崌偼10/11偱偡丅偟偨偑偭偰10倗偺悈傪尭傜偡偨傔偵偼丄10亐10/11亖11倗偺怘墫悈傪幪偰傞昁梫偑偁傝傑偡丅 嘇 嘆偱尭偭偰偟傑偭偨怘墫傪捛壛偟傑偡丅 嘆偵傛偭偰11倗偺怘墫悈傪幪偰丄悈傪10倗尭傜偡偙偲偼偱偒傑偟偨偑丄摨帪偵侾倗偺怘墫傕幪偰偰偟傑偭偰偄傑偡丅仏幪偰偨11倗偺怘墫悈乧悈10倗亄怘墫侾倗 偮傑傝嵟屻偵侾倗偺怘墫傪捛壛偡傞偙偲偱丄柍帠偵戣堄偺嶌傝捈偟偼姰椆偟傑偡丅 仏偙偺栤戣偼戞63島嵗偱庢傝忋偘偨偙偲偑偁傝傑偟偨丅偁傢偣偰偛嶲峫偔偩偝偄丅 |